ОЧЕНЬ
Начертите рисунки по координатам :
1)(-7;-6) , (-7;4) , (-5;6) , (3;6) , (9;8) , (9,10) , (11;8) , (13;8) , (15;6)
2)(15;8) , (16;6) , (17;6) , (17;8) , (19;6) , (19;4) , (16;2) , (13;2) , (9;0).
3) (10;-6) , (5;-6) , (5;-2) , (-2;-2) , (-2;-6) , (-7;-6)
а) 1) 26×5 = 130 (Б.) - продали во 2 день
2) 26+130 = 156 (б.) - продали в третий день
3) 26 + 130 + 156 = 312 (б.) продали за три дня
ответ : 312 билетов
Б) В магазин привозили овощи в течении пяти дней. Каждый день привозили одинаковое количество овощей. Сколько всего стало овощей, если каждый день привозили по 26 штук, но в последний день купили ещё 26 овощей?
Решение: 26×5- 26 = 104 (ов.) стало
ответ : 104 овоща.
Ещё одна задача :
На фабрику привезли 5 рулонов ткани по 26 метров в каждом. На пальто ушло 26 метров. Сколько метров осталось ткани?
Я докажу первое и последнее, остальное - сам.
1)
Доказательство "⇒".
Пусть у нас дано ((A∪B)⊂C), докажем тогда, что
1.1) A⊂C,
и
1.2) B⊂C.
1.1) x∈A⊂A∪B, ⇒ x∈A∪B⊂С, ⇒ x∈C. То есть A⊂C.
1.2) x∈B⊂A∪B, ⇒ x∈A∪B⊂C, ⇒ x∈C. То есть B⊂C.
чтд.
Доказательство "<=".
Пусть у нас дано: A⊂C и B⊂C. Докажем тогда, что
A∪B⊂C.
Пусть x∈A∪B, ⇔ x∈A или x∈B.
a) x∈A⊂C, ⇒ x∈C.
б) x∈B⊂C, ⇒ x∈C.
То есть A∪B⊂C.
чтд.
4)
Доказательство "⇒".
Пусть у нас дано (A⊂(B∪C)). Докажем тогда, что
Пусть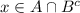 , ⇔
, ⇔ 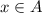 и
и 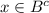 , ⇔
, ⇔
Тогда т.к. A⊂B∪C, имеем
Первый случай. Если x∈B и x∉B, то x∈∅⊂C ⇒ x∈C.
Второй случай. Если x∈C и x∉B, то x∈C\B⊂C, ⇒ x∈C.
чтд.
Доказательство "<=".
Пусть у нас дано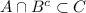 , докажем тогда, что
, докажем тогда, что
A⊂ B∪C.
Пусть x∈A. Тут возможны два варианта x∈B, либо x∉B.
Случай первый: x∈A и x∈B, ⇒ x∈A∩B⊂B, ⇒ x∈B⊂B∪C, ⇒ x∈B∪C.
Случай второй: x∈A и x∉B, ⇒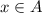 и
и 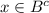 , ⇒
, ⇒
⇒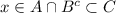 , ⇒ x∈C⊂B∪C, ⇒ x∈B∪C.
, ⇒ x∈C⊂B∪C, ⇒ x∈B∪C.
чтд.