Один конец отрезка находится в начальной точке координатной системы O(0;0).
Другой конец A имеет координаты (28;0).
Определи координаты серединной точки C отрезка OA..
2. Один конец отрезка находится в начальной точке координатной системы O(0;0).
Другой конец B имеет координаты (0;2).
Определи координаты серединной точки D отрезка OB.
3. Один конец отрезка находится в точке M с координатами (28;2), другой конец N имеет координаты (18;38).
Определи координаты серединной точки K отрезка MN.
Игрок участвует хотя бы в одном из двух подряд идущих раундов. Игрок участвует в двух подряд идущих раундах при условии победы в первом из них.
Найдем общее число раундов:
Алиса участвовала в 10 раундах, соответственно, в 11 не участвовала.
Если Алиса не побеждала, то она участвовали либо во всех четных, либо во всех нечетных раундах. Так как она участвовала в 10 раундах, то значит это были четные раунды: 2, 4, ..., 20.
Предположим, что Алиса победила ровно 1 раз. Пусть это произошло в раунде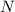
. Тогда вместо участия в раундах 
, 
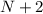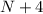, ..., 20 из предыдущего условия она должна будет участвовать в раундах 
, 
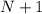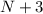, ..., 19. По нашему предположению в 19 раунде она также проиграет и будет участвовать в 21 раунде. Но тогда общее число раундов, в которых он участвовала будет равно 11. Противоречие. Значит, выиграть ровно 1 раз она не могла.
Аналогично, выиграть более одного раза она тем более не могла.
Значит, Алиса проиграла во всех своих раундах, в том числе и во втором.
ответ : Алиса
Игрок участвует хотя бы в одном из двух подряд идущих раундов. Игрок участвует в двух подряд идущих раундах при условии победы в первом из них.
Найдем общее число раундов:
Алиса участвовала в 10 раундах, соответственно, в 11 не участвовала.
Если Алиса не побеждала, то она участвовали либо во всех четных, либо во всех нечетных раундах. Так как она участвовала в 10 раундах, то значит это были четные раунды: 2, 4, ..., 20.
Предположим, что Алиса победила ровно 1 раз. Пусть это произошло в раунде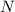
. Тогда вместо участия в раундах 
, 
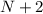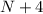, ..., 20 из предыдущего условия она должна будет участвовать в раундах 
, 
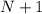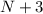, ..., 19. По нашему предположению в 19 раунде она также проиграет и будет участвовать в 21 раунде. Но тогда общее число раундов, в которых он участвовала будет равно 11. Противоречие. Значит, выиграть ровно 1 раз она не могла.
Аналогично, выиграть более одного раза она тем более не могла.
Значит, Алиса проиграла во всех своих раундах, в том числе и во втором.
ответ : Алиса