Вначале переводим смешанную дробь в неправильную дробь.
1) 124 * 1700 = 210 800
2) 210 800 + 1665 = 212 465
У нас получается дробь 212 465/ 1700
Далее мы должны привести знаменатель 1700 к знаменателю равному 10, 100, 1000, 10 000 и т.д. Если, например, у нас будет дробь 5/20, мы сможем перевести ее в десятичную дробь, так как 20 можно привести к знаменателю 100, умножив на 5. Числитель мы умножаем на число, на которое умножаем 20, то есть на 5. В итоге у нас получается дробь 25/100. Чтобы выразить эту дробь как десятичную, мы смотрим, нет ли у дроби целого числа. В нашем случае его нет. У нас получается число 0 целых 25/100. Записывается оно следующим образом: 0, 25. Но, если бы у нас было число 0 целых 5/100, мы бы записали его так: 0, 05. Ведь в цифре пяти 1 разряд, а в числе 100 3 разряда. Например, если у нас будет дробь 5/1000, то мы запишем ее так: 0, 005.
Вернемся к нашему примеру. После подборов на калькуляторе, можно выяснить, что дробь 212 465/ 1700 не приводятся к знаменателям 10, 100, 1000, 10 000 и т.д. Поэтому ее нельзя превратить в десятичную дробь.
124,9794117647, такой примерный ответ выходит при решении на калькуляторе.
Задача №1. Пусть камушков лежало во 2 кучке, тогда в 1 кучке лежало камушков. В 2 кучах всего лежит камушка.
Составим и решим уравнение по данным условиям:
Значит всего во 2 кучке лежало камушков. Но это только часть ответа к нашей задаче!
Мы нашли кол-во камушков только во 2 кучке, а у нас есть ещё и 1 кучка! Мы сможем это сделать, подставив в выражение для 1 кучки, которое мы составляли для уравнения, значение .
Т.е. камешков лежало в 1 кучке.
Проверка:
камушка в 2 кучках (задаче решена верно).
Вот теперь можно сказать, что: Задача решена! ☑
ответ: в 1 кучке лежало камушков, а во 2 кучке камушков.
Задача №2. Пусть первое целое число, тогда если числа последовательные, то следующие 3 целых числа буду равны , и . Их сумма равна .
Составим и решим уравнение по данным условиям:
Значит 1 целое число равно . Но это снова только часть ответа к нашей задаче!
Мы нашли только 1 целое число, а нам нужно узнать ещё и 2, и 3, и 4. Мы сможем это сделать, подставив в каждое выражение, составленное для 2, 3 и 4 числа к уравнению, значение . То есть:
Вначале переводим смешанную дробь в неправильную дробь.
1) 124 * 1700 = 210 800
2) 210 800 + 1665 = 212 465
У нас получается дробь 212 465/ 1700
Далее мы должны привести знаменатель 1700 к знаменателю равному 10, 100, 1000, 10 000 и т.д. Если, например, у нас будет дробь 5/20, мы сможем перевести ее в десятичную дробь, так как 20 можно привести к знаменателю 100, умножив на 5. Числитель мы умножаем на число, на которое умножаем 20, то есть на 5. В итоге у нас получается дробь 25/100. Чтобы выразить эту дробь как десятичную, мы смотрим, нет ли у дроби целого числа. В нашем случае его нет. У нас получается число 0 целых 25/100. Записывается оно следующим образом: 0, 25. Но, если бы у нас было число 0 целых 5/100, мы бы записали его так: 0, 05. Ведь в цифре пяти 1 разряд, а в числе 100 3 разряда. Например, если у нас будет дробь 5/1000, то мы запишем ее так: 0, 005.
Вернемся к нашему примеру. После подборов на калькуляторе, можно выяснить, что дробь 212 465/ 1700 не приводятся к знаменателям 10, 100, 1000, 10 000 и т.д. Поэтому ее нельзя превратить в десятичную дробь.
124,9794117647, такой примерный ответ выходит при решении на калькуляторе.
Составим и решим уравнение по данным условиям:
Значит всего во 2 кучке лежало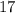 камушков. Но это только часть ответа к нашей задаче!
камушков. Но это только часть ответа к нашей задаче!
Мы нашли кол-во камушков только во 2 кучке, а у нас есть ещё и 1 кучка! Мы сможем это сделать, подставив в выражение для 1 кучки, которое мы составляли для уравнения, значение .
.
Т.е.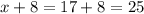 камешков лежало в 1 кучке.
камешков лежало в 1 кучке.
Проверка:
Вот теперь можно сказать, что: Задача решена! ☑
ответ: в 1 кучке лежало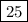 камушков, а во 2 кучке
камушков, а во 2 кучке  камушков.
камушков.
Задача №2. ПустьСоставим и решим уравнение по данным условиям:
Значит 1 целое число равно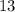 . Но это снова только часть ответа к нашей задаче!
. Но это снова только часть ответа к нашей задаче!
Мы нашли только 1 целое число, а нам нужно узнать ещё и 2, и 3, и 4. Мы сможем это сделать, подставив в каждое выражение, составленное для 2, 3 и 4 числа к уравнению, значение . То есть:
. То есть:
Проверка:
Вот теперь можно сказать, что: Задача решена! ☑
ответ: 1 число -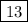 , 2 число -
, 2 число -  , 3 число -
, 3 число - 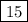 , 4 число -
, 4 число - 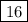 .
.