Мода ряда (Мо) - наиболее часто встречающееся число ряда.
В данном ряду мода отсутствует, т.к. все числа ряда представлены 1 раз.
Медиана ряда (Ме) - число, стоящее в середине ряда. Т.к. ряд состоит из чётного количества элементов, то медианой будет среднее арифметическое двух чисел, стоящих в середине ряда:
Ме=(0+2):2=2:2=1
Среднее арифметическое ряда - это среднее арифметическое чисел данного ряда:
Хср.=(-3+(-2)+0+2+3+4):6=4:6=2/3≈0,67
2) 6, 5, -2, 4, -5, 0
Упорядочим данный числовой ряд:
-5; -2; 0; 4; 5; 6
Мода ряда (Мо) - наиболее часто встречающееся число ряда.
В данном ряду мода отсутствует, т.к. все числа ряда представлены 1 раз.
Медиана ряда (Ме) - число, стоящее в середине ряда. Т.к. ряд состоит из чётного количества элементов, то медианой будет среднее арифметическое двух чисел, стоящих в середине ряда:
Ме=(0+4):2=4:2=2
Среднее арифметическое ряда - это среднее арифметическое чисел данного ряда:
1) 4, -3, 2, 0, 3, -2
Упорядочим данный числовой ряд:
-3; -2; 0; 2; 3; 4
Мода ряда (Мо) - наиболее часто встречающееся число ряда.
В данном ряду мода отсутствует, т.к. все числа ряда представлены 1 раз.
Медиана ряда (Ме) - число, стоящее в середине ряда. Т.к. ряд состоит из чётного количества элементов, то медианой будет среднее арифметическое двух чисел, стоящих в середине ряда:
Ме=(0+2):2=2:2=1
Среднее арифметическое ряда - это среднее арифметическое чисел данного ряда:
Хср.=(-3+(-2)+0+2+3+4):6=4:6=2/3≈0,67
2) 6, 5, -2, 4, -5, 0
Упорядочим данный числовой ряд:
-5; -2; 0; 4; 5; 6
Мода ряда (Мо) - наиболее часто встречающееся число ряда.
В данном ряду мода отсутствует, т.к. все числа ряда представлены 1 раз.
Медиана ряда (Ме) - число, стоящее в середине ряда. Т.к. ряд состоит из чётного количества элементов, то медианой будет среднее арифметическое двух чисел, стоящих в середине ряда:
Ме=(0+4):2=4:2=2
Среднее арифметическое ряда - это среднее арифметическое чисел данного ряда:
Хср.=(-5+(-2)+0+4+5+6):6=8:6=4/3≈1,33
№ 4. x ≤ 0.75
№ 5. ( - ∞; - 1 ] ∪ [ 3; + ∞ )
Пошаговое объяснение:
№ 4.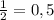
Тогда выражение имеет вид:
(0,5)^ (2*x) ≥ (0.125) ^ (1/2)
(0.5) ^ (2*x) ≥ ((0.5)^3)^(1/2)
(0.5) ^ (2*x) ≥ (0.5) ^ (3*(1/2)
(0.5) ^ (2*x) ≥ (0.5) ^ (3/2)
(0.5) ^ (2*x) ≥ (0.5) ^ 1.5
Т.к. 0,5 < 1, то имеем:
2 * х ≤ 1.5
x ≤ 1.5 / 2
x ≤ 0.75 или иначе записать можно так х ≤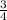
№ 5. 7 ^ (x ^ 2) * 49 ^ ( - x) ≥ 343
7 ^ (x ^ 2) * 7^2^ ( - x) ≥ 7 ^ 3
7 ^ (x ^ 2) * 7^ ( - 2 * x) ≥ 7 ^ 3
7 ^ ((x ^ 2) + ( - 2 * x)) ≥ 7 ^ 3
7 ^ (x ^ 2 - 2 * x) ≥ 7 ^ 3
Т.к. 7 > 1, то запишем так:
x ^ 2 - 2 * x ≥ 3
Решим получившееся квадратное неравенство.
x ^ 2 - 2 * x = 3
x ^ 2 - 2 * x - 3 = 0
D = 16
x1,2 = (2±4)/2
x1 = 3 и x2 = -1
Решим методом интервалов.
( - ∞; - 1 ] ∪ [ 3; + ∞ )