Для того чтобы найти наименьшее общее кратное натуральных чисел нужно: 1) разложить эти числа на простые множители; 2) Выписать разложение одного из чисел; 3) дополнить его новыми множителями из другого разложения; 4) найти полученное произведение. У нас есть разложение чисел на простые множители: 1) a = 2 * 3 и b = 2 * 7, тогда НОК ( а; b ) = 2 * 3 * 7 = 42; 2) c = 2 * 2 * 5 и d = 3 * 3 * 5. тогда НОК ( с; d ) = 3 * 3 * 5 * 2 * 2 = 180; 3) e = 2 * 2 * 5 и f = 2 * 3 * 5, тогда НОК ( е; f ) = 2 * 2 * 5 * 3 = 60.
В длинных выражениях с различными знаками вычитания, сложения, умножения и деления, первым делом упрощается то, что находится в скобках.
1- Поэтому первым действием будет вычитание в левой скобке:
2 - Преобразуем правую скобку по такому же принципу:
3 -Теперь вернёмся в левую часть выражения и поделим получившуюся разность в скобке 115,6 на 10:.
Представим данное выражение в виде двух дробей: 115,6 переведем в неправильную дробь, где получим , а число десять представим в виде дроби . Теперь запишем данное деление в ином виде:
При делении двух дробей, вторая "переворачивается" и происходит их умножение:
4 -Теперь итог правой дроби умножим на 3:
Получили две неправильные дроби с одинаковым знаменателем.
5 - Теперь мы легко можем вычесть из первой дроби вторую:
Для того чтобы найти наименьшее общее кратное натуральных чисел нужно: 1) разложить эти числа на простые множители; 2) Выписать разложение одного из чисел; 3) дополнить его новыми множителями из другого разложения; 4) найти полученное произведение. У нас есть разложение чисел на простые множители: 1) a = 2 * 3 и b = 2 * 7, тогда НОК ( а; b ) = 2 * 3 * 7 = 42; 2) c = 2 * 2 * 5 и d = 3 * 3 * 5. тогда НОК ( с; d ) = 3 * 3 * 5 * 2 * 2 = 180; 3) e = 2 * 2 * 5 и f = 2 * 3 * 5, тогда НОК ( е; f ) = 2 * 2 * 5 * 3 = 60.
Пошаговое объяснение:
Нам дано выражение:
В длинных выражениях с различными знаками вычитания, сложения, умножения и деления, первым делом упрощается то, что находится в скобках.
1- Поэтому первым действием будет вычитание в левой скобке:
2 - Преобразуем правую скобку по такому же принципу:
3 -Теперь вернёмся в левую часть выражения и поделим получившуюся разность в скобке 115,6 на 10: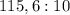
.
Представим данное выражение в виде двух дробей: 115,6 переведем в неправильную дробь, где получим
, а число десять представим в виде дроби 
. Теперь запишем данное деление в ином виде:
При делении двух дробей, вторая "переворачивается" и происходит их умножение:
4 -Теперь итог правой дроби умножим на 3:
Получили две неправильные дроби с одинаковым знаменателем.
5 - Теперь мы легко можем вычесть из первой дроби вторую: