Определите координаты рисунка ​

(см. объяснение)

Пошаговое объяснение:

Вынесении общего множителя за скобки.

Рассмотрим пример:

Хорошо видно, что и 24 и 16 делятся на 8. Тогда 8 - это общий множитель, который можно вынести за скобки. Далее делим исходное выражение на 8 и отправляем полученное в скобки.

Попробуйте решить самостоятельно:

(ответы в конце объяснения)

Вынесении многочлена за скобки:

Прием тут аналогичен описанному выше.

Рассмотрим пример:

Здесь все то же самое, только за скобки выносится общая часть.

При этом не нужно бояться выражения в скобках!

Если оно одинаково, то смело пользуйтесь приемом:

Каким бы страшным не показалось семикласснику это выражение, прием остается 100% таким же!

Группировка.

Рассмотрим пример:

Здесь необходимо представить 2x, как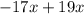 . После чего воспользоваться знаниями выше.

Иногда сразу дают выражение вида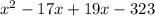 , что упрощает ситуацию.

ответы к заданиям для самостоятельного решения.

Объяснение завершено!

1) 6x + 6y + ax + ay

Группируем слагаемые по группам (x-ы и y-и, и выносим их за скобку)

6x + ax + 6y + ay = x (6 + a) + y (6 + a)

Выносим общую часть в обоих слагаемых за скобку

(6 + a) (x + y)

2) По тому же принципу сокращаем это выражение (Думаю понятно уже как, поэтому просто распишу решение)

(x^2)y + x + (y^2)x + y = x(xy + 1) + y(xy + 1) = (y+x)(yx+1)

3) Бла-бла тот же принцип, группируем выносим общее число, у получившихся слагаемых также выносим общее число

(9a^2)b + 3a^2 - 3b^2 - b = 3a^2(3b + 1) - b (3b + 1) = (3a^2 -b) (3b + 1)

Минус потому-что мы вынесли не только b но -b, чтобы можно было сократить общее число в дальнейшем (чтобы был + и +, а не + и -)