Доказать тавтологию - значит показать, что при всех истинностных значениях булевых переменных логическое выражение будет принимать только значение ИСТИНА.
Для первого логического выражения составляем таблицу (F - ЛОЖЬ, T - ИСТИНА):
Видно, что последний столбец, соответствующий заданному логическому выражению, состоит только из значений ИСТИНА при любом наборе булевых переменных.
Для второго логического выражения также составляем таблицу:
Видно, что последний столбец, соответствующий заданному логическому выражению, состоит только из значений ИСТИНА при любом наборе булевых переменных.
Таблица для третьего логического выражения:
Видно, что последний столбец, соответствующий заданному логическому выражению, состоит только из значений ИСТИНА при любом наборе булевых переменных.
То, что решается через характеристическое уравнение - это общее решение. Оно всегда будет независимо от правой части диффура.
По сути, нужно найти так называемое частное решение, и тогда решением для этого диффура будет сумма общего и частного решений.
Частное решение подбирается, исходя из правой части. В данном случае, правая часть есть многочлен второго порядка. Поэтому частное решение будет также иметь вид многочлена, причем многочлена второго порядка: ( - частное решение, A, B и C - константы, которые нужно подобрать). Теперь необходимо подставить это решение вместо y в данном диффуре, и найти константы.
(второго порядка потому, что многочлена первого порядка может не хватать, а многочлен не ниже третьего порядка избыточен, можешь попробовать подставить многочлен третьего порядка, но при нахождении коэффициентов он занулится)
UPD: ошибся в выборе многочена. Нужно использовать многочлен третьего порядка: (необходимо, чтобы после подстановки в диффур в левой части получился многочлен не ниже порядка многочлена в правой части)
Пошаговое объяснение:
Доказать тавтологию - значит показать, что при всех истинностных значениях булевых переменных логическое выражение будет принимать только значение ИСТИНА.
Для первого логического выражения составляем таблицу (F - ЛОЖЬ, T - ИСТИНА):
Видно, что последний столбец, соответствующий заданному логическому выражению, состоит только из значений ИСТИНА при любом наборе булевых переменных.
Для второго логического выражения также составляем таблицу:
Видно, что последний столбец, соответствующий заданному логическому выражению, состоит только из значений ИСТИНА при любом наборе булевых переменных.
Таблица для третьего логического выражения:
Видно, что последний столбец, соответствующий заданному логическому выражению, состоит только из значений ИСТИНА при любом наборе булевых переменных.
То, что решается через характеристическое уравнение - это общее решение. Оно всегда будет независимо от правой части диффура.
По сути, нужно найти так называемое частное решение, и тогда решением для этого диффура будет сумма общего и частного решений.
Частное решение подбирается, исходя из правой части. В данном случае, правая часть есть многочлен второго порядка. Поэтому частное решение будет также иметь вид многочлена, причем многочлена второго порядка: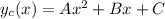 (
(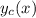 - частное решение, A, B и C - константы, которые нужно подобрать). Теперь необходимо подставить это решение вместо y в данном диффуре, и найти константы.
- частное решение, A, B и C - константы, которые нужно подобрать). Теперь необходимо подставить это решение вместо y в данном диффуре, и найти константы.
(второго порядка потому, что многочлена первого порядка может не хватать, а многочлен не ниже третьего порядка избыточен, можешь попробовать подставить многочлен третьего порядка, но при нахождении коэффициентов он занулится)
UPD: ошибся в выборе многочена. Нужно использовать многочлен третьего порядка: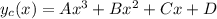 (необходимо, чтобы после подстановки
(необходимо, чтобы после подстановки 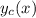 в диффур в левой части получился многочлен не ниже порядка многочлена в правой части)
в диффур в левой части получился многочлен не ниже порядка многочлена в правой части)