Опытный велосипедист доехал от Алматы до обсерватории , которая расположена на плато Ассы-Тургень в 100 км от города за 4 часа,а на обратном пути он уменьшил скорость на 5 км/ч. Сколько времени он потратил на обратный путь?
Математика и спорт, казалось бы, далеки друг от друга. Но это только на первый взгляд. Многие представители различных наук и, в частности, математики и физики старшего поколения с большим вниманием относятся к своим спортивным занятиям. Знают они, что занятия спортом гармоническому развитию личности, что спорт закаляет человека физически и духовно.
За последние десятилетия произошли существенные изменения условий жизни, произошел качественный скачок в образовании, особенно в области точных наук. Возросший поток информации увеличил психологические нагрузки в сфере служебных обязанностей; занятия в школе стали более напряженными. Новые условия жизни, учебы и работы потребовали от молодежи определенной психологической и физической устойчивости.
Норберт Винер, считал, что ему лучше всего писалось, когда умственная работа чередовалась с простыми, не требующими умственной нагрузки удовольствиями — прогулками, плаванием. Поклонникам интеллектуальных игр полезно знать, что в спорте и спортивных играх ум, образование, расчет — вещи далеко не лишние. Математические методы все шире используются в спорте. Трудно себе представить, сколько еще нерешенных проблем возникает при рассмотрении взаимодействия мяча и ракетки, мяча с грунтом или травой.
Известно, что методами математической статистики устанавливают перспективность спортсменов, условия, наиболее благоприятные для тренировок, их эффективность, обрабатывают показания датчиков, контролирующих нагрузки спортсменов. Теория информации позволяет оценить степень загруженности зрительного аппарата при занятиях различными видами спорта. Математика и физика изыскивать наиболее удачные формы гребных судов и весел.
В то же время занятие спортом благотворно влияют на умственную деятельность и психику человека, укрепляют его волю. Этот факт бесспорен для многих ученых.
Можно утверждать, что удивительное творческое долголетие многих наших выдающихся математиков и физиков обеспечивается их дружбой со спортом
Применение в различных видах спорта
Имеются рекомендации по созданию оптимальной программы еженедельных тренировок для пятиборцев.
Построенная модель включала в качестве целевой функции линейную зависимость от результатов в каждом виде пятиборья. В качестве ограничений фигурировали также линейные зависимости, среди которых — ограничение на общее время (в течение недели) тренировок спортсмена по всем пяти видам спорта; на объем скоростных тренировок — он не может быть меньше объема тренировок на выносливость; на объем тренировок по общей физической подготовке — он должен превышать объем тренировок по отработке техники и т. п. Возникшая модель "анализировалась методами линейного программирования.
Существует математическая модель соревнования по подъему штанги. Нарочно упрощенная модель предполагала, что каждый из спортсменов имеет право попытаться лишь один раз взять вес и лишь один раз пропустить подход к очередному (или начальному) весу. В рамках этой модели выявились оптимальные стратегии участников соревнований. Аналогичным методом может быть проанализирована ситуация, фактически имеющая место в соревнованиях, когда каждый участник получает право на три попытки поднять штангу.
Примерно теми же методами можно изучить ситуацию, возникающую в соревнованиях по прыжкам в высоту и прыжкам с шестом, в которых каждый из участников имеет право а) начать прыжки с любой высоты, но не меньшей, чем фиксированная «квалификационная»; б) сделать три попытки для преодоления каждой следующей установленной высоты. Преодолев некоторую «начальную» высоту (он ее выбирает сам), спортсмен просит поднять планку и т. д. Ему засчитывается наибольшая из преодоленных высот, без учета предшествующих попыток. Если спортсмен начинает выступление с большей начальной высоты, то он экономит силы, и вероятность взятия следующей высоты увеличивается. Однако в случае неудачной попытки его результат считается нулевым. Имеется возможность оценить в вероятностных терминах ожидаемый результат спортсмена в зависимости от начальной высоты и выдать некоторые рекомендации относительно оптимальной начальной высоты.
Тем самым математика тесно связано со спортом, и без математики никуда
Пошаговое объяснение:
это степенной ряд. запишем его в общем виде
областью сходимости степенного ряда является интервал (-R;R), где R - радиус сходимости и равен
посчитаем этот предел
таким образом, ряд является сходящимся (абсолютно) при всех x, принадлежащих интервалу (-7;7)
теперь посмотрим сходимость ряда на концах этого интервала.
пусть х = -7, тогда мы получим ряд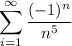
, это числовой знакочередующийся ряд
надо исследовать его на сходимость. исследуем по признаку Лейбница
а) по первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего
б) по второму признаку Лейбница предел ряда по модулю должен стремится к 0
т.е. ряд сходится x = -7 - точка сходимости
теперь пусть х = 7
тогда всё просто, как в первом случае, только ряд не знакочередующийся. он сходится x = 7 - точка сходимости
и вот получаем,
данный степенной ряд является сходящимся на интервале [-7;7]
Доклад
Математика и спорт, казалось бы, далеки друг от друга. Но это только на первый взгляд. Многие представители различных наук и, в частности, математики и физики старшего поколения с большим вниманием относятся к своим спортивным занятиям. Знают они, что занятия спортом гармоническому развитию личности, что спорт закаляет человека физически и духовно.
За последние десятилетия произошли существенные изменения условий жизни, произошел качественный скачок в образовании, особенно в области точных наук. Возросший поток информации увеличил психологические нагрузки в сфере служебных обязанностей; занятия в школе стали более напряженными. Новые условия жизни, учебы и работы потребовали от молодежи определенной психологической и физической устойчивости.
Норберт Винер, считал, что ему лучше всего писалось, когда умственная работа чередовалась с простыми, не требующими умственной нагрузки удовольствиями — прогулками, плаванием. Поклонникам интеллектуальных игр полезно знать, что в спорте и спортивных играх ум, образование, расчет — вещи далеко не лишние. Математические методы все шире используются в спорте. Трудно себе представить, сколько еще нерешенных проблем возникает при рассмотрении взаимодействия мяча и ракетки, мяча с грунтом или травой.
Известно, что методами математической статистики устанавливают перспективность спортсменов, условия, наиболее благоприятные для тренировок, их эффективность, обрабатывают показания датчиков, контролирующих нагрузки спортсменов. Теория информации позволяет оценить степень загруженности зрительного аппарата при занятиях различными видами спорта. Математика и физика изыскивать наиболее удачные формы гребных судов и весел.
В то же время занятие спортом благотворно влияют на умственную деятельность и психику человека, укрепляют его волю. Этот факт бесспорен для многих ученых.
Можно утверждать, что удивительное творческое долголетие многих наших выдающихся математиков и физиков обеспечивается их дружбой со спортом
Применение в различных видах спорта
Имеются рекомендации по созданию оптимальной программы еженедельных тренировок для пятиборцев.
Построенная модель включала в качестве целевой функции линейную зависимость от результатов в каждом виде пятиборья. В качестве ограничений фигурировали также линейные зависимости, среди которых — ограничение на общее время (в течение недели) тренировок спортсмена по всем пяти видам спорта; на объем скоростных тренировок — он не может быть меньше объема тренировок на выносливость; на объем тренировок по общей физической подготовке — он должен превышать объем тренировок по отработке техники и т. п. Возникшая модель "анализировалась методами линейного программирования.
Существует математическая модель соревнования по подъему штанги. Нарочно упрощенная модель предполагала, что каждый из спортсменов имеет право попытаться лишь один раз взять вес и лишь один раз пропустить подход к очередному (или начальному) весу. В рамках этой модели выявились оптимальные стратегии участников соревнований. Аналогичным методом может быть проанализирована ситуация, фактически имеющая место в соревнованиях, когда каждый участник получает право на три попытки поднять штангу.
Примерно теми же методами можно изучить ситуацию, возникающую в соревнованиях по прыжкам в высоту и прыжкам с шестом, в которых каждый из участников имеет право а) начать прыжки с любой высоты, но не меньшей, чем фиксированная «квалификационная»; б) сделать три попытки для преодоления каждой следующей установленной высоты. Преодолев некоторую «начальную» высоту (он ее выбирает сам), спортсмен просит поднять планку и т. д. Ему засчитывается наибольшая из преодоленных высот, без учета предшествующих попыток. Если спортсмен начинает выступление с большей начальной высоты, то он экономит силы, и вероятность взятия следующей высоты увеличивается. Однако в случае неудачной попытки его результат считается нулевым. Имеется возможность оценить в вероятностных терминах ожидаемый результат спортсмена в зависимости от начальной высоты и выдать некоторые рекомендации относительно оптимальной начальной высоты.
Тем самым математика тесно связано со спортом, и без математики никуда
Пошаговое объяснение: