Орасидаги масофа 450 км/с булган юк ва енгил автомашина бир бирига караб йулга чикди ва 3соатдан кейин учрашишди енгил автомашинанинг тезлиги юк машина тезлигидан 30км/с ортик булса унинг тезлиги ни топинг
Умножим уравнение xy = -12 на два и сложим со вторым уравнением:
Теперь вычтем из второго уравнения удвоенное первое:
Заметим, что если - решение, то - тоже решение в силу четности, и - тоже решение в силу симметрии. Поэтому достаточно найди найти одно любое решение и автоматически можно будет записать все остальные.
Возьмем к примеру равенства и запишем новую систему . Складываем оба уравнения и получаем, что . Подставляем , к примеру, в первое уравнение и получаем, что .
Пара - решение. В силу описанной выше особенности системы подбираем еще 3 решения: , и /
Решать можно было и без симметрии и четности. Для этого достаточно к записанной выше системе дописать еще три: . Если их решить, то получим все те же пары решений.
В стране волшебников живут волшебники и волшебницы.
Каждый знаком друг с другом.
У одного волшебника столько знакомых волшебников, сколько и волшебниц.
У волшебницы вдвое меньше знакомых волшебниц, чем волшебников. Сколько волшебников и волшебниц в стране волшебства?
________________________________________________________
Решение.
х - волшебников;
у - волшебниц
Так как каждый знаком друг с другом, то у каждого волшебника все волшебницы знакомые, и все волшебники знакомые кроме него самого.
Получим первое уравнение:
х - 1 = у
Аналогично для каждой волшебницы:
х = 2 · (у-1)
Решаем систему:
Подставим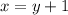 во второе уравнение:
во второе уравнение:
3 волшебницы в стране волшебства.
4 волшебника в стране волшебства.
ответ: 4 волшебника;
3 волшебницы.
Умножим уравнение xy = -12 на два и сложим со вторым уравнением:
Теперь вычтем из второго уравнения удвоенное первое:
Заметим, что если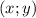 - решение, то
- решение, то 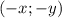 - тоже решение в силу четности, и
- тоже решение в силу четности, и 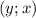 - тоже решение в силу симметрии. Поэтому достаточно найди найти одно любое решение и автоматически можно будет записать все остальные.
- тоже решение в силу симметрии. Поэтому достаточно найди найти одно любое решение и автоматически можно будет записать все остальные.
Возьмем к примеру равенства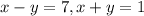 и запишем новую систему
и запишем новую систему 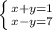 . Складываем оба уравнения и получаем, что
. Складываем оба уравнения и получаем, что 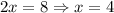 . Подставляем
. Подставляем  , к примеру, в первое уравнение и получаем, что
, к примеру, в первое уравнение и получаем, что 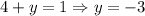 .
.
Пара - решение. В силу описанной выше особенности системы подбираем еще 3 решения:
- решение. В силу описанной выше особенности системы подбираем еще 3 решения: 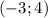 ,
, 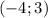 и
и 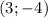 /
/
Решать можно было и без симметрии и четности. Для этого достаточно к записанной выше системе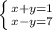 дописать еще три:
дописать еще три: 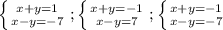 . Если их решить, то получим все те же пары решений.
. Если их решить, то получим все те же пары решений.
ОТВЕТ: (4; -3), (-3; 4), (-4; 3), (3; -4).