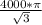Т.к. осевое сечение является правильным треугольником, а радиус основания r равен 10, значит все стороны это треугольника равны 20. Опустим высоту из вершины этого треугольника и найдем ее длину по теореме Пифагора: h==10. Теперь найдем площадь треугольника, зная его высоту, а радиус основания конуса будет половиной основания этого треугольника: S=hr=20*10=100
Объем конуса равен V=*h. Радиус основания r и высота конуса h нам уже известны. Подставляем значения: V=100*10=
а) 100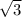 б)
б) 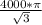
Пошаговое объяснение:
Т.к. осевое сечение является правильным треугольником, а радиус основания r равен 10, значит все стороны это треугольника равны 20. Опустим высоту из вершины этого треугольника и найдем ее длину по теореме Пифагора: h= =10
=10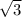 . Теперь найдем площадь треугольника, зная его высоту, а радиус основания конуса будет половиной основания этого треугольника: S=
. Теперь найдем площадь треугольника, зная его высоту, а радиус основания конуса будет половиной основания этого треугольника: S=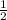 hr=
hr=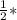 20*10
20*10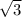 =100
=100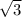
Объем конуса равен V=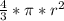 *h. Радиус основания r и высота конуса h нам уже известны. Подставляем значения: V=
*h. Радиус основания r и высота конуса h нам уже известны. Подставляем значения: V=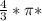 100*10
100*10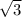 =
=