Дано: АВСД- піраміда, ΔАСВ, ∠С=90°,АС=6 см, СВ=8 см, всі бічні грані утворюють кут 60 з площиною основи∠γ=60°.
Знайти: ДО-?
Рішення : так як усі бічні грані утворюють кут в 60°, то вершина Д проецирується у центр кола, описаного навколо ΔАСВ. Так як ΔАСВ- прямокутний, то за властивістю центр кола О знаходиться на гіпотенузі ΔАСВ та ділить її навпіл .
Гіпотенуза АВ=10см ( за теоремою Піфагора , або єгипетьсий трикутник 3,4,5 із коєффіцієнтом 2: 6,8,10)
Відповідь:
5√3 см
Покрокове пояснення:
Дано: АВСД- піраміда, ΔАСВ, ∠С=90°,АС=6 см, СВ=8 см, всі бічні грані утворюють кут 60 з площиною основи∠γ=60°.
Знайти: ДО-?
Рішення : так як усі бічні грані утворюють кут в 60°, то вершина Д проецирується у центр кола, описаного навколо ΔАСВ. Так як ΔАСВ- прямокутний, то за властивістю центр кола О знаходиться на гіпотенузі ΔАСВ та ділить її навпіл .
Гіпотенуза АВ=10см ( за теоремою Піфагора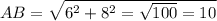 , або єгипетьсий трикутник 3,4,5 із коєффіцієнтом 2: 6,8,10)
, або єгипетьсий трикутник 3,4,5 із коєффіцієнтом 2: 6,8,10)
Розглянемо ΔАДО, ∠О=90°, ∠А=∠γ=60°, А0= АВ:2=40см:2=5см.
tg 60°= ДО/АО;
ДО=АО*tg 60°=5см*√3=5√3 см