Основа прямого паралелепіпеда паралелограм зі сторонами 5 і 8 см та гострим кутом 30 °. площа повної поверхности паралелепіпеда = 170смс знайти висоту паралелепіпеда
Пусть не так, и Р и Q - многочлены степени не ниже 1.
- парабола с вершиной в точке , ветви направлены вверх.
- парабола с вершиной в точке , ветви направлены вверх.
Пусть подобными действиями было получено значение
Выберем . Получим, что
Т.е. построена монотонно возрастающая последовательность такая, что . Очевидно, т.к. последовательность не ограничена сверху, то в ней бесконечное число членов => многочлен принимает значение в бесконечном числе точек => тогда он будет иметь вид , а значит его степень бесконечна, что невозможно.
А тогда , откуда , следовательно . Т.е. на множестве с бесконечным числом элементов многочлен принимает значение . А тогда, по аналогии с предыдущим пунктом,
ответ
Р = 2 * (а + в),
S = a * в,
1.
длина прямоугольника 12 м, а площадь - 96 м².
найти ширину прямоугольника и его периметр.
в = S : а = 96 : 12 = 8 м - ширина,
Р = 2 * (12 + 8) = 2 * 20 = 40 м - периметр,
2.
ширина прямоугольника 20 см, а площадь - 860 см².
найти длину прямоугольника и его периметр.
а = S : в = 860 : 20 = 43 см - длина,
Р = 2 * (20 + 43) = 2 * 63 = 126 см - периметр,
3.
длина прямоугольника 30 м, а площадь - 750 м².
найти ширину прямоугольника и его периметр.
в = S : а = 750 : 30 = 25 м - ширина,
Р = 2 * (30 + 25) = 2 * 55 = 110 м - периметр,
4.
длина прямоугольника 60 см, а площадь - 720 см².
найти ширину прямоугольника и его периметр.
в = S : а = 720 : 60 = 12 см - ширина,
Р = 2 * (60 + 12) = 2 * 72 = 144 см - периметр
Пусть не так, и Р и Q - многочлены степени не ниже 1.
Пусть подобными действиями было получено значение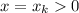
Выберем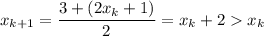 . Получим, что
. Получим, что 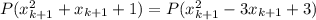
Т.е. построена монотонно возрастающая последовательность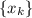 такая, что
такая, что 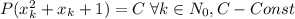 . Очевидно, т.к. последовательность не ограничена сверху, то в ней бесконечное число членов => многочлен
. Очевидно, т.к. последовательность не ограничена сверху, то в ней бесконечное число членов => многочлен 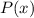 принимает значение
принимает значение 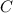 в бесконечном числе точек => тогда он будет иметь вид
в бесконечном числе точек => тогда он будет иметь вид 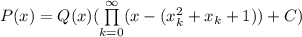 , а значит его степень бесконечна, что невозможно.
, а значит его степень бесконечна, что невозможно.
А тогда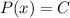 , откуда
, откуда 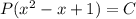 , следовательно
, следовательно 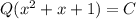 . Т.е. на множестве
. Т.е. на множестве 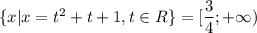 с бесконечным числом элементов многочлен
с бесконечным числом элементов многочлен 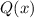 принимает значение
принимает значение 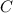 . А тогда, по аналогии с предыдущим пунктом,
. А тогда, по аналогии с предыдущим пунктом, 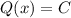
Ч.т.д.