Чтобы умножить дробь на дробь, нужно умножить числитель на числитель, а знаменатель на знаменатель, и первое произведение сделать чисдителем результата, а второе - знаменателем.
Пример 1.
· =
Если умножаются смешанные числа, то их предварительно обращают в неправильные дроби.
Пример 2.
1 · 2 = · = = 4
Примечание. А если умножаем на целое число, то представляем его в виде дроби со знаменателем 1.
Чтобы разделить дробь на дробь, нужно числитель первой дроби умножить на знаменатель второй дроби, а знаменатель первой дроби умножить на знаменатель второй дроби, и первое произведение сделать числителем результата, а второе произведение - знаменателем результата.
Пример 3.
1 : 1 = : = · = = 1
Чтобы найти величину дроби (части) данного числа, нужно данное число умножить на эту дробь.
Задача 1.
Для отопления дома заготовили 8 кубометров дров, а израсходовали лишь запаса. Сколько кубометров дров было израсходовано?
Решение.
8 · = = 6 м³
ответ: было израсходовано 6 м³ дров.
Чтобы найти число по данной величине дроби, нужно данную величину разделить на эту дробь.
Задача 2.
Скосили 2 гектара травы, что составляет площади всего луга. Какова площадь луга в гектарах?
Решение.
2 : = 2 · = 3 га
ответ: площадь луга 3 га.
2. ДЕСЯТИЧНЫЕ ДРОБИ
Чтобы умножить десятичные дроби, достаточно, не обращая внимания на запятые, перемножить их как целые числа, и в полученном произведении отделить справа запятой столько знаков, сколько их было отделено в обоих сомножителях вместе.
Пример 4.
2,25 · 1,12 = 2,5200 = 2,52
Объяснение.
Сначала мы умножили 225 на 112 - получили 25200.
Посчитали, сколько знаков было справа от запятой: в первом числе - 2 знака, во втором числе - тоже 2 знака, итого - 4 знака.
Значит, в полученном числе 25200 надо справа отделить 4 знака. Получаем 2,5200. Так как последние нули обычно не пишут, то ответ можно записать как 2,52.
Чтобы разделить дробь на дробь, надо и в делимом и в делителе перенести запятую вправо на одно и то же количество знаков, чтобы оба числа стали целыми числами, а затем разделить. Если в одном из чисел знаков меньше, то сначала приписываем нули.
Пример 5.
72,9 : 0,09 = 72,90 : 0,09 = 7290 : 9 = 810
Объяснение.
Здесь мы приписали к числу 72,9 один ноль, затем перенесли запятую вправо на 2 знака, после чего разделили числа.
См. Пошаговое объяснение
Пошаговое объяснение:
1. ОБЫКНОВЕННЫЕ ДРОБИ
Чтобы умножить дробь на дробь, нужно умножить числитель на числитель, а знаменатель на знаменатель, и первое произведение сделать чисдителем результата, а второе - знаменателем.
Пример 1.
Если умножаются смешанные числа, то их предварительно обращают в неправильные дроби.
Пример 2.
1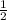
· 2
= 
· 
= 
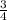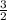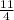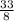= 4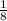
Примечание. А если умножаем на целое число, то представляем его в виде дроби со знаменателем 1.
Чтобы разделить дробь на дробь, нужно числитель первой дроби умножить на знаменатель второй дроби, а знаменатель первой дроби умножить на знаменатель второй дроби, и первое произведение сделать числителем результата, а второе произведение - знаменателем результата.
Пример 3.
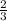1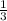
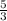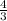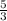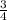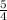: 1
= 
: 
= 
· 
= 
= 1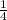
Чтобы найти величину дроби (части) данного числа, нужно данное число умножить на эту дробь.
Задача 1.
Для отопления дома заготовили 8 кубометров дров, а израсходовали лишь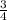
запаса. Сколько кубометров дров было израсходовано?
Решение.
8 ·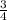
= 
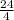= 6 м³
ответ: было израсходовано 6 м³ дров.
Чтобы найти число по данной величине дроби, нужно данную величину разделить на эту дробь.
Задача 2.
Скосили 2 гектара травы, что составляет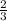
площади всего луга. Какова площадь луга в гектарах?
Решение.
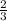2 :
= 2 ·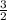 
= 3 га
ответ: площадь луга 3 га.
2. ДЕСЯТИЧНЫЕ ДРОБИ
Чтобы умножить десятичные дроби, достаточно, не обращая внимания на запятые, перемножить их как целые числа, и в полученном произведении отделить справа запятой столько знаков, сколько их было отделено в обоих сомножителях вместе.
Пример 4.
2,25 · 1,12 = 2,5200 = 2,52
Объяснение.
Сначала мы умножили 225 на 112 - получили 25200.
Посчитали, сколько знаков было справа от запятой: в первом числе - 2 знака, во втором числе - тоже 2 знака, итого - 4 знака.
Значит, в полученном числе 25200 надо справа отделить 4 знака. Получаем 2,5200. Так как последние нули обычно не пишут, то ответ можно записать как 2,52.
Чтобы разделить дробь на дробь, надо и в делимом и в делителе перенести запятую вправо на одно и то же количество знаков, чтобы оба числа стали целыми числами, а затем разделить. Если в одном из чисел знаков меньше, то сначала приписываем нули.
Пример 5.
72,9 : 0,09 = 72,90 : 0,09 = 7290 : 9 = 810
Объяснение.
Здесь мы приписали к числу 72,9 один ноль, затем перенесли запятую вправо на 2 знака, после чего разделили числа.
Первый столбец:
0,1 см = 1 * 10^-1 * 10^-2 м
2,5 м = 25 * 10^-1* 10^2 см
0,25 м = 25 * 10^-2 * 10^3 мм
0,006 мм^2 = 6 * 10^-3 * 10^-2 см^2
0,7 мм^2 = 7 * 10^-1 * 10^-6 м^2
2000 см^2 = 2 * 10^3 * 10^-4 м^2
3000 см^2 = 3 * 10^3 * 10^2 мм^2
2134 м^2 = 2134 * 10^4 см^2
0,2134 м^2 = 2134 * 10^-4 * 10^6 мм^2
9 мм^3 = 9 * 10^-3 см^3
9000 мм^3 = 9 * 10^3 * 10^-9 м^3
0,009 см^3 = 9 * 10^-3 * 10^-6 м^3
0,009 см^3 = 9 * 10^-3 * 10^3 мм^3
0,0009 м^3 = 9 * 10^-4 * 10^6 см^3
0,000000009 м^3 = 9 * 10^-9 * 10^9 мм^3
Второй столбец:
9 км = 9 * 10^3 м
0,9 км = 9 * 10^-1 * 10^5 см
72,4 км = 724 * 10^-1 * 10^3 м
7000 м = 7 * 10^3 * 10^-3 км
0,0007 см = 7 * 10^-4 * 10^-5 км
7000000 мм = 7 * 10^6 * 10^-6 км
0,02 км^2 = 2 * 10^-2 * 10^6 м^2
0,00005 км^2 = 5 * 10^-5 * 10^10 см^2
2 * 10^4 км^2 = 2 * 10^4 * 10^12 мм^2
3 * 10^-3 км^3 = 3 * 10^-3 * 10^9 м^3
3 км^3 = 3 * 10^15 см^3
3 * 10^-10 км^3 = 3 * 10^-10 * 10^18 мм^3
10^9 м^3 = 10^9 * 10^-9 км^3
10^15 cм^3 = 10^15 * 10^-15 км^3
4 * 10^14 мм^3 = 4 * 10^14 * 10^-18 км^3