Ozingiz bilgan mashhur insonlar nomlarini tuzing va ular qanday ixtirolar qiganliklarini yozing

Показать ответ

Ответ:

Сателла1

02.03.2023 01:09

Пошаговое объяснение:

№1

1-2/9=9/9-2/9=7/9 (осталось выполнить)

№2

70/105 (Сокращаем на 5)=14/21 (Сокращаем на 7)=1/3

№3

1/7+3/4 (домножаем для общего знаменателя 28)=4/28+21/28=25/28

№4

$\frac{1114}{-4/35}$ =1114*(-35)/4=-38990/4 (сокращаем на 2)=-19495/2=-9747 $\frac{1}{2}$ =-9747,5

№5

7/25*5=35/25 (сокращаем на 5)=7/5=1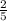 $\frac{2}{5}$ =1,4

№6

9/28:18/35=(9*35)/(28*18) сокращаем 9 и 18 (делим на 9)=35/56=5/8

№7

5/6*х=4(1/2)

х=4(1/2)/(5/6)

х=27/5=5,4

№8

7/8*7/8=49/64

№9

5/7*35=25 (см)

№10

4(5/11)*22/98=49/11*22/98 (сокращаем (49 и 98) и (11 и 22))=2/2=1

№11

60/2*5=150

№12

Всего 68 га

Первый день 68*1/4=17 га

Второй день (68-17)*2/3=34 га

Третий день 68-17-34=17 га

№13

(7/12+11/30х):7/14=1/3

(7/12+11/30х)*14/7=1/3

22/30х=1/3-14/12

22/30х=-5/6

х=-25/22=-1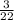 $\frac{3}{22}$

0,0(0 оценок)

Ответ:

kovtunenkoone

03.10.2020 11:06

6) приравниваем выражение под модулем к нулю. x=3/4

Нарисуем интервал и разобьём его на 2 отрезка: (-беск. до 3/4] и (3/4 до +беск.)

Берём из первого интервала любое число, например -100. Подставляем в выражение 4x-3. Получается отрицательное число, значит знак на интервале (-беск. до 3/4] "-".

Аналогично, для второго интервала, берём число 100, подставляем. Знак интервала (3/4 до +беск.) "+".

Раскрываем модуль на 1-ом интервале:

-7/3(4x-3)+7,2=9

x= 39/70

Проверяем на интервале (-беск. до 3/4]

Данное число входит в этот интервал, значит является корнем.

Также на 2-ом, со знаком "+".

7/3(4x-3)+7,2=9

x=33/35

Проверяем на интервале (3/4 до +беск.). Данный корень является решением

ответ: x=39/70, x2=33/35

0,0(0 оценок)