Вспомним такую известную нам операцию как сложение нескольких одинаковых слагаемых. Например, 5 + 5 + 5. Такую запись математик заменит более короткой:
5 ∙ 3. Или 7 + 7 + 7 + 7 + 7 + 7 запишет как 7 ∙ 6
А писать а + а + а + …+ а (где n слагаемых а) – вообще не будет, а напишет а ∙ n. Точно так же математик не будет длинно писать произведение нескольких одинаковых множителей. Произведение 2 ∙ 2 ∙ 2 запишется как 23 (2 в третьей степени). А произведение 4 ∙ 4 ∙ 4 ∙ 4 ∙ 4 ∙ 4 как 46(4 в шестой степени). Но если необходимо, то можно короткую запись заменить более длинной. Например, 74 (7 в четвёртой степени) записать как 7∙7∙7∙7. Теперь дадим определение.
Под записью аn (где n – натуральное число) понимают произведение n множителей, каждый из которых равен а.
Саму запись аn называют степенью числа а, число а – основанием степени, число n – показателем степени.
Запись аn можно прочитать как «а в энной степени» или как «а в степени эн». Записи а2 (а во второй степени) можно прочитать как « а в квадрате», а запись а3 ( а в третьей степени) можно прочитать как «а в кубе». Ещё один особый случай – это степень с показателем 1. Здесь необходимо отметить следующее:
Степенью числа а с показателем 1 называют само это число. Т.е. а1 = а.
Любая степень числа 1 равна 1.
т.е. 1n = 1. Например, 15 = 1; 145 = 1.
Любая степень числа 0 равна 0. Т.е. 0n = 0. Например, 07 = 0; 021 = 0.
А теперь давайте рассмотрим несколько степеней с основанием 10.
103 = 1000
104 = 10000
106 = 1000000
Вы заметили, что степени десяти – это единица с таким количеством нулей, каков показатель степени?
Всего возможны две ситуации: из конверта в конверт будет переложена простая задача или задача повышенной сложности.
Рассмотрим случай, когда будет переложена простая задача.
Найдем вероятность того, что из первого конверта во второй будет переложена простая задача. Для этого разделим число простых задач на общее количество задач в первом конверте:
После такого перекладывания во втором конверте окажется 5 простых задач и 8 задач повышенной сложности. Достать из такого конверта простую задачу можно с вероятностью:
Но такой конверт получается только с вероятностью . Значит итоговая вероятность достать простую задачу при условии, что переложена была простая задача равна:
Рассмотрим случай, когда будет переложена задача повышенной сложности.
Найдем вероятность того, что из первого конверта во второй будет переложена задача повышенной сложности:
После такого перекладывания во втором конверте окажется 4 простые задачи и 9 задач повышенной сложности. Достать из такого конверта простую задачу можно с вероятностью:
Но такой конверт получается только с вероятностью . Значит итоговая вероятность достать простую задачу при условии, что переложена была простая задача равна:
Поскольку события "переложить простую задачу" и "переложить задачу повышенной сложность" - несовместные, то общая вероятность достать простую задачу:
Пошаговое объяснение:
Вспомним такую известную нам операцию как сложение нескольких одинаковых слагаемых. Например, 5 + 5 + 5. Такую запись математик заменит более короткой:
5 ∙ 3. Или 7 + 7 + 7 + 7 + 7 + 7 запишет как 7 ∙ 6
А писать а + а + а + …+ а (где n слагаемых а) – вообще не будет, а напишет а ∙ n. Точно так же математик не будет длинно писать произведение нескольких одинаковых множителей. Произведение 2 ∙ 2 ∙ 2 запишется как 23 (2 в третьей степени). А произведение 4 ∙ 4 ∙ 4 ∙ 4 ∙ 4 ∙ 4 как 46(4 в шестой степени). Но если необходимо, то можно короткую запись заменить более длинной. Например, 74 (7 в четвёртой степени) записать как 7∙7∙7∙7. Теперь дадим определение.
Под записью аn (где n – натуральное число) понимают произведение n множителей, каждый из которых равен а.
Саму запись аn называют степенью числа а, число а – основанием степени, число n – показателем степени.
Запись аn можно прочитать как «а в энной степени» или как «а в степени эн». Записи а2 (а во второй степени) можно прочитать как « а в квадрате», а запись а3 ( а в третьей степени) можно прочитать как «а в кубе». Ещё один особый случай – это степень с показателем 1. Здесь необходимо отметить следующее:
Степенью числа а с показателем 1 называют само это число. Т.е. а1 = а.
Любая степень числа 1 равна 1.
т.е. 1n = 1. Например, 15 = 1; 145 = 1.
Любая степень числа 0 равна 0. Т.е. 0n = 0. Например, 07 = 0; 021 = 0.
А теперь давайте рассмотрим несколько степеней с основанием 10.
103 = 1000
104 = 10000
106 = 1000000
Вы заметили, что степени десяти – это единица с таким количеством нулей, каков показатель степени?
Всего возможны две ситуации: из конверта в конверт будет переложена простая задача или задача повышенной сложности.
Рассмотрим случай, когда будет переложена простая задача.
Найдем вероятность того, что из первого конверта во второй будет переложена простая задача. Для этого разделим число простых задач на общее количество задач в первом конверте:
После такого перекладывания во втором конверте окажется 5 простых задач и 8 задач повышенной сложности. Достать из такого конверта простую задачу можно с вероятностью:
Но такой конверт получается только с вероятностью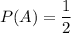 . Значит итоговая вероятность достать простую задачу при условии, что переложена была простая задача равна:
. Значит итоговая вероятность достать простую задачу при условии, что переложена была простая задача равна:
Рассмотрим случай, когда будет переложена задача повышенной сложности.
Найдем вероятность того, что из первого конверта во второй будет переложена задача повышенной сложности:
После такого перекладывания во втором конверте окажется 4 простые задачи и 9 задач повышенной сложности. Достать из такого конверта простую задачу можно с вероятностью:
Но такой конверт получается только с вероятностью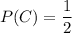 . Значит итоговая вероятность достать простую задачу при условии, что переложена была простая задача равна:
. Значит итоговая вероятность достать простую задачу при условии, что переложена была простая задача равна:
Поскольку события "переложить простую задачу" и "переложить задачу повышенной сложность" - несовместные, то общая вероятность достать простую задачу:
ответ: 9/26