Это показательное уравнение вида , где неизвестная переменная.
Если сделаем основания степени равными, то по правилу сможем приравнять показатели степеней и решить обычное линейное уравнение.
Для этого, нужно член уравнения представить в виде числа со степенью так, чтобы в основании было число . Это явно число (проверка: ).
Значит теперь, когда наше показательное уравнение имеет вид , то можем приравнять показатели степени и получим стандартное линейное уравнение. Решение этого уравнения и будет являться корнем исходного показательного уравнения.
Итак, мы получили уравнение после того, как приравняли показатели степени. Решаем это уравнение. Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое. Т.е. .
Из этого следует, что ответ нашего показательного уравнения равен .
Ещё раз говорю не в ту тему вночишь, это первое, во вторых тебе перевод надо? указывай конкретно, если перевод то вот он: соединенные штаты несколько дней каждый год в ознаменование событий, людей или общественных мероприятиях. эти дни называются праздниками. технически, в сша не празднуют национальные праздники, но конгресс назначил 10 "официальные праздничные дни", во время которой большинство федеральных учреждений закрыты и большинство федеральных служащих не работают. начиная с 1971 года, ряд из них были исправлены по понедельникам, с тем чтобы позволить трудящимся длинных праздничных выходных семь из федерального законные праздники — новый год; вашингтон день рождения/ день президента; день памяти; день независимости; день труда; день и рождество — почти повсеместно в государственном и частном секторах они считаются американская любимых праздников. новый год (1 января) — американцы празднуют начало нового года дома, в кругу друзей, и в посиделках от турнир парад роз в калифорнии для гигантской соберутся в нью-йорке на таймс-сквер. день рождения вашингтона (третий понедельник февраля) — день рождения джорджа вашингтона, первого президента сша, был законный выходной с 1885 года. ряд государств также отметили 1 февраля — день рождения авраама линкольна, 16-го президента. некоторые законодатели выступали за объединение двух событий в один праздник. многие американцы сейчас называют праздника "день президентов", - в честь вашингтона и линкольна и всех президентов. день памяти (последний понедельник мая) — это праздник чтит погибших во всех военных конфликтах. закон о единых праздничные дни, установленные федеральным законный отпуск, зафиксированный в понедельник, начало в 1971 году. всех 50 штатах соблюдать праздник день независимости (4 июля) — день независимости празднуется в честь принятия декларации независимости вторым континентальным конгрессом 4 июля 1776. день труда (первый понедельник сентября) — день труда празднуется вклад трудящихся мужчин и женщин. для многих американцев этот праздник выделяет неофициальным окончанием лета и началом учебного года. день (четвертый четверг ноября) — вариант праздники урожая отмечают этот праздник в четвертый четверг ноября. день обычно отмечается в условиях. остается поводом для большой и праздничной трапезы, и для того, чтобы выразить , за то, что баунти. рождество (25 декабря) — большинство протестанты и римо-католики и некоторые православные христиане празднуют рождение иисуса 25 декабря. рождество отмечают дома, с украшением и дисплей вечнозеленых елок, и с семьями и детьми, обмениваясь подарками и карт.
Это показательное уравнение вида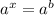 , где
, где 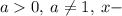 неизвестная переменная.
неизвестная переменная.
Если сделаем основания степени равными, то по правилу сможем приравнять показатели степеней и решить обычное линейное уравнение.
Для этого, нужно член уравнения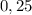 представить в виде числа со степенью так, чтобы в основании было число
представить в виде числа со степенью так, чтобы в основании было число 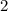 . Это явно число
. Это явно число 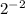 (проверка:
(проверка: 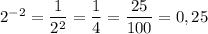 ).
).
Значит теперь, когда наше показательное уравнение имеет вид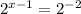 , то можем приравнять показатели степени и получим стандартное линейное уравнение. Решение этого уравнения и будет являться корнем исходного показательного уравнения.
, то можем приравнять показатели степени и получим стандартное линейное уравнение. Решение этого уравнения и будет являться корнем исходного показательного уравнения.
Итак, мы получили уравнение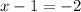 после того, как приравняли показатели степени. Решаем это уравнение. Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое. Т.е.
после того, как приравняли показатели степени. Решаем это уравнение. Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое. Т.е. 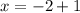 .
.
Из этого следует, что ответ нашего показательного уравнения равен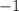 .
.
ответ: