Рассмотрим только кратчайшие пути. Пусть паук сидит в А1, а муха в С. Если паук пройдет по ребру A1A, то у него будет 3 пути: ADC, ABC, AC. Тоже самое, если он пройдет по ребру A1B1 или A1D1. По 3 на каждую. Всего 3*3 = 9 путей. Если он пройдет сначала по диагонали A1D, то у него будет 5 путей: DC, DAC, DBC, DC1C, DD1C. И также на каждой из 3 диагоналей. Всего 3*5 = 15 путей. Итак, получается всего 9 + 15 = 24 кратчайших путей. Есть и более длинные пути, например, A1ABB1C1C или A1DD1B1C. Таких путей очень много, я даже не знаю, как их все пересчитать.
Число противоположное равно числу, противоположному , то есть . К числу мы прибавляем :
(Противоположное число - число, которое на числовой прямой имеет такое же расстояние от 0, что у данного, но он стоит по другую сторону от 0, например, противоположное число 5 равно -5, так как на числовой прямой у них одинаковое расстояние до 0 (расстояние равно 5), но 5 стоит справа от 0, а противоположное должно стоять по другую сторону, то есть слева, Число, стоящее слева от нуля и имеющее расстояние 5 равно -5).
Если паук пройдет по ребру A1A, то у него будет 3 пути: ADC, ABC, AC.
Тоже самое, если он пройдет по ребру A1B1 или A1D1. По 3 на каждую.
Всего 3*3 = 9 путей.
Если он пройдет сначала по диагонали A1D, то у него будет 5 путей:
DC, DAC, DBC, DC1C, DD1C.
И также на каждой из 3 диагоналей. Всего 3*5 = 15 путей.
Итак, получается всего 9 + 15 = 24 кратчайших путей.
Есть и более длинные пути, например, A1ABB1C1C или A1DD1B1C.
Таких путей очень много, я даже не знаю, как их все пересчитать.
14
Пошаговое объяснение:
Число противоположное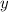
равно числу, противоположному 
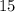, то есть 
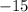. К числу 
мы прибавляем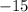 
:
(Противоположное число - число, которое на числовой прямой имеет такое же расстояние от 0, что у данного, но он стоит по другую сторону от 0, например, противоположное число 5 равно -5, так как на числовой прямой у них одинаковое расстояние до 0 (расстояние равно 5), но 5 стоит справа от 0, а противоположное должно стоять по другую сторону, то есть слева, Число, стоящее слева от нуля и имеющее расстояние 5 равно -5).
ответ: 14