Отрицательные числа всегда меньше, чем положительные:1. 1) -4,5<3;Ноль больше любого отрицательного числа, но меньше любого положительного:2) 0>-1;Чем ближе отрицательное число стоит к нулю, тем оно больше того, которое дальше:3) -0,4<-0,401;Чтобы сравнить десятичные и обыкновенные дроби, то нужно перевести их к одному виду:4)-2,8 = -2 целых 8/10 =-2 и 16/20-2 и 16/20 > -2 и 17/20;2. -6,12<-6,08<-6,02;3. -6<х<2, х₁∈{-5; -4; -3; -2; -1; 0; 1}; х<-4, х₂∈(-∞; -5)х₁∩х₂={-5}
Пошаговое объяснение:
Отрицательные числа всегда меньше, чем положительные:1. 1) -4,5<3;Ноль больше любого отрицательного числа, но меньше любого положительного:2) 0>-1;Чем ближе отрицательное число стоит к нулю, тем оно больше того, которое дальше:3) -0,4<-0,401;Чтобы сравнить десятичные и обыкновенные дроби, то нужно перевести их к одному виду:4)-2,8 = -2 целых 8/10 =-2 и 16/20-2 и 16/20 > -2 и 17/20;2. -6,12<-6,08<-6,02;3. -6<х<2, х₁∈{-5; -4; -3; -2; -1; 0; 1}; х<-4, х₂∈(-∞; -5)х₁∩х₂={-5}
Пошаговое объяснение:
7. ВСего в совете 2+4+5= 11 членов.
Разных подкомитетов по 3 из этих 11 можно создать
С = 11!/(8!3!)=9*10*11/(2*3) =3*5*11=165
2-х технологов из 5 можно набрать С
и 1 менеджера из 4 можно выбрать 4-мя
Итого подкомитет из 1 менеджера и 2-х технологов можно выбрать
Тогда вероятность набора такого подкомитета равна
Р( 1 менеджер и 2 технолога)= 40/165 =8/33
8. a) Если купит один и второй не купит, то такая ситуация может образоваться 2-мя
1-ый купит, а второй нет , либо второй купит , а первый нет.
Вероятность первой ситуации P(1-ый купит)*Р(2-ой не купит)=
0.65*(1-0.56)= 0.65*0.44=0.286
Вероятность второй ситуации P(2-ый купит)*Р(1-ый не купит)=
(1-0.65)*0.56= 0.35*0.56=0.196
Итого полная вероятность Р(только один купит)=0.286+0.196=0.482
б) Вероятность того, что купит хоть один равна 1- вероятность того, что ни один не купит.
Р(не купит ни один)=(1-0.65)*(1-0.56)=0.35*0.44=0.154
Р(купит хоть один)= 1-0.154=0.846
9. Вычисляем по формуле Бернулли
P(n;k)= С(n;k)*p =2000!/(1460!*540!) *0.75
=2000!/(1460!*540!) *0.75 =
=
=2000!/(1460!*540!)*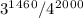 =
=