1 - 63. 2 - 81. 3 - 66
Пошаговое объяснение:
Количество помидоров в первом ящике - 30% от 210 = 63кг
Кол-во помидоров на 2 и 3 ящик - 210-63=147
Можно решить данную задачу уравнением.
Пусть х - кол-во помидоров в 3 ящике, тогда во втором будет 1х. Общее кол-во помидоров - 147. Составляем уравнение:
1 5/22x + x = 147
27/22x+x=147
+ = 147
x=147
умножим обе части на 22/49 чтобы избавиться от дроби
x = 22*3
x = 66
Так мы получили, что в 3 ящике 66 кг помидоров. Во втором - 66* 1 = 15 (это на столько больше) 66+15=81.
а) - 2;5
б) х 1 ( внизу) = -6 , х 2 ( внизу) = 2
а) 2;6 ( х - 2) = 1;8 ( х - 4)
2;6 х - 5;2 = 1;8 ( х -4)
Переносим неизвестную в левую часть и нужно сменить её знак
2;6 х - 5;2 - 1;8х = -7;2
Переносим постоянную в правую часть и нужно сменить знак её
2;6 - 1;8 х = -7;2 + 5;2
Приводим подобные члены
0;8 х= - 7;2 + 5;2
0; 8 х = - 2
Разделим обе стороны уравнения на 0;8
х = - 2; 5
б) | 2 х+4 | = 8
Используя определение модуля, представим уравнение с модулем в виде двух отдельных уравнений
2 х+ 4 = 8
2 х+ 4 = -8
Решаем уравнение относительно х
х = 2
2х + 4 = - 8
х= 2
х = -6
Уравнение имеет 2 решения
х 1 = -6 , х 2 = 2
1 - 63. 2 - 81. 3 - 66
Пошаговое объяснение:
Количество помидоров в первом ящике - 30% от 210 = 63кг
Кол-во помидоров на 2 и 3 ящик - 210-63=147
Можно решить данную задачу уравнением.
Пусть х - кол-во помидоров в 3 ящике, тогда во втором будет 1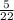 х. Общее кол-во помидоров - 147. Составляем уравнение:
х. Общее кол-во помидоров - 147. Составляем уравнение:
1 5/22x + x = 147
27/22x+x=147
умножим обе части на 22/49 чтобы избавиться от дроби
x = 22*3
x = 66
Так мы получили, что в 3 ящике 66 кг помидоров. Во втором - 66* 1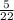 = 15 (это на столько больше) 66+15=81.
= 15 (это на столько больше) 66+15=81.
а) - 2;5
б) х 1 ( внизу) = -6 , х 2 ( внизу) = 2
Пошаговое объяснение:
а) 2;6 ( х - 2) = 1;8 ( х - 4)
2;6 х - 5;2 = 1;8 ( х -4)
Переносим неизвестную в левую часть и нужно сменить её знак
2;6 х - 5;2 - 1;8х = -7;2
Переносим постоянную в правую часть и нужно сменить знак её
2;6 - 1;8 х = -7;2 + 5;2
Приводим подобные члены
0;8 х= - 7;2 + 5;2
0; 8 х = - 2
Разделим обе стороны уравнения на 0;8
х = - 2; 5
х = - 2; 5
б) | 2 х+4 | = 8
Используя определение модуля, представим уравнение с модулем в виде двух отдельных уравнений
2 х+ 4 = 8
2 х+ 4 = -8
Решаем уравнение относительно х
х = 2
2х + 4 = - 8
х= 2
х = -6
Уравнение имеет 2 решения
х 1 = -6 , х 2 = 2