Для решения интегралов подобного вида обычно используют формулу Ньютона-Лейбница:
В данном случае , а также и . Все это можем подставить в формулу и выполнить действия:
Задача решена!
Для решения интегралов подобного вида обычно используют формулу Ньютона-Лейбница:
В данном случае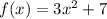 , а также
, а также 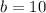 и
и 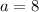 . Все это можем подставить в формулу и выполнить действия:
. Все это можем подставить в формулу и выполнить действия:
Задача решена!
ответ: 502 .