Расстояние от вершины В до плоскости - перпендикуляр, опущенный из этой вершины на плоскость.Точку пересечения перпендикуляра с плоскостью обозначим буквой F. Сторона треугольника AC и точка F лежат в одной плоскости. AF и CF являются соответственно проекциями сторон АВ и СВ. Рассмотрим треугольник ABF или треугольник CBF. Это прямоугольные треугольники, согласно теореме (если прямая перпендикулярна плоскости..). AB=10cм -сторона равностороннего треугольника, BF= 8см, найдем AF, которая является проекцией стороны АВ. AF²=AB²-ВF² AF²=10²-8²=100-64=36 AF=6
Заметим, что каждому такому числу можно сопоставить другое число, заменив цифру a на b и наоборот (например, числу соответствует число ). Рассмотрим сумму двух таких чисел. Для этого распишем их в развёрнутой форме: , . Их сумма равна . Она делится на 11111. Любая такая сумма делится на 11111, поскольку если перед некоторым множителем 10ⁿ в одном числе стоит a, то в другом — обязательно b, и в сумме получаем (a + b)·10ⁿ. Поскольку сумма каждой такой пары делится на 11111, то и сумма сумм (без повторений) тоже будет делиться на 11111, но сумма таких сумм — это все числа, удовлетворяющие условию задачи.
AF²=AB²-ВF²
AF²=10²-8²=100-64=36
AF=6
Да
Пошаговое объяснение:
Заметим, что каждому такому числу можно сопоставить другое число, заменив цифру a на b и наоборот (например, числу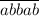
соответствует число 
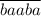). Рассмотрим сумму двух таких чисел. Для этого распишем их в развёрнутой форме: 
, 
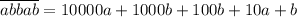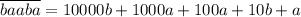. Их сумма равна 
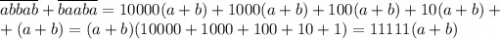. Она делится на 11111. Любая такая сумма делится на 11111, поскольку если перед некоторым множителем 10ⁿ в одном числе стоит a, то в другом — обязательно b, и в сумме получаем (a + b)·10ⁿ. Поскольку сумма каждой такой пары делится на 11111, то и сумма сумм (без повторений) тоже будет делиться на 11111, но сумма таких сумм — это все числа, удовлетворяющие условию задачи.