Имеем дело с однородной СЛАУ, у которой кол-во неизвестных больше кол-ва уравнений, значит, имеем нетривиальные решения.
Приведем матрицу к ступенчатому виду:
Меняем 1 и 3 строки:
Вычитаем из второй строки первую, умноженную на 7:
Делим на -2 вторую строку и прибавляем к 3 строке первую, умноженную на 4:
Вычитаем из 3 строки вторую:
Вычитаем из 2 строки третью:
Вычитаем из 3 строки вторую, умноженную на 4:
Ранг равен трем, откуда количество свободных переменных равно 4 - 3 = 1. Пусть D - свободная переменная. Тогда
Значит,
ответ: векторы вида , при .
а)0,68*3\4=68\100*3\4=17*3\100=51\100
б)3,212\(4\5) = 3212\1000\(4\5)=3212\1000*5\4=803\200=4 целых 15\1000
в)5\6*24,6=5\6*246\10=41\2=20 целых 5\10=20 целых 1\2
г)0,121\(11\12)=121\1000*12\11=11*12\1000=132\1000=0,132
д)43,75*2\35 =43 целых 75\100*2\35 =4375\100*2\35=125\50=25\10=5\2=2,5
е) 13\21*8,4=13\21*84\10=13*4\10=52\10=26\5=5,2
ж)5,6\(3 целых 1\2)=56\10\(7\2)=56\10*2\7=8\5=1,6
з)10 целых 2\3 *6,3=32\10*6 целых 3\10=32\3*63\10=21*16\5=336\5=67 целых 2\10=67 целых 1\5
и) 2 целых 3\20 *4,2 =43\20*42\10=43*21\100=903\100=9 целых 3\100
к)2,3\1,5 +6,7\4,5=2 целых 3\10 (1 целая 5\10)+6 целых 7\10\(4 целых 5\10)=
=23\10\(15\10)+67\10\(45\10)=(23\10*10\15)+(67\10*10\45) = 23\15+(67\45)=
=23*3+67\45 =136\45=3 целых 1\45
л) 1,5\3,2 + (1,9\9,6) =1 целая 5\10\(3 целых 2\10) +(1 целая 9\10\9 целых 6\10)=(15\10*10\32)+(19\10*10\96) =15\32+19\96 =15*3+19\96=64\96=32\48=4\6=2\3
м)7,4\5,7 -9,1\11,4 =(74\10\57\10)-(91\10\114\10) =(74\10*10\57) -(91\10*10\114)=74\57 -91\114=74*2-91\114=57\114=1\2=0,5
Имеем дело с однородной СЛАУ, у которой кол-во неизвестных больше кол-ва уравнений, значит, имеем нетривиальные решения.
Приведем матрицу к ступенчатому виду:
Меняем 1 и 3 строки:
Вычитаем из второй строки первую, умноженную на 7:
Делим на -2 вторую строку и прибавляем к 3 строке первую, умноженную на 4:
Вычитаем из 3 строки вторую:
Вычитаем из 2 строки третью:
Вычитаем из 3 строки вторую, умноженную на 4:
Ранг равен трем, откуда количество свободных переменных равно 4 - 3 = 1. Пусть D - свободная переменная. Тогда
Значит,
ответ: векторы вида![\tilde{D}\left[\begin{array}{c}9\\-17\\5\\43\end{array}\right]](/tpl/images/1148/9647/1e9f9.png) , при
, при 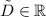 .
.
а)0,68*3\4=68\100*3\4=17*3\100=51\100
б)3,212\(4\5) = 3212\1000\(4\5)=3212\1000*5\4=803\200=4 целых 15\1000
в)5\6*24,6=5\6*246\10=41\2=20 целых 5\10=20 целых 1\2
г)0,121\(11\12)=121\1000*12\11=11*12\1000=132\1000=0,132
д)43,75*2\35 =43 целых 75\100*2\35 =4375\100*2\35=125\50=25\10=5\2=2,5
е) 13\21*8,4=13\21*84\10=13*4\10=52\10=26\5=5,2
ж)5,6\(3 целых 1\2)=56\10\(7\2)=56\10*2\7=8\5=1,6
з)10 целых 2\3 *6,3=32\10*6 целых 3\10=32\3*63\10=21*16\5=336\5=67 целых 2\10=67 целых 1\5
и) 2 целых 3\20 *4,2 =43\20*42\10=43*21\100=903\100=9 целых 3\100
к)2,3\1,5 +6,7\4,5=2 целых 3\10 (1 целая 5\10)+6 целых 7\10\(4 целых 5\10)=
=23\10\(15\10)+67\10\(45\10)=(23\10*10\15)+(67\10*10\45) = 23\15+(67\45)=
=23*3+67\45 =136\45=3 целых 1\45
л) 1,5\3,2 + (1,9\9,6) =1 целая 5\10\(3 целых 2\10) +(1 целая 9\10\9 целых 6\10)=(15\10*10\32)+(19\10*10\96) =15\32+19\96 =15*3+19\96=64\96=32\48=4\6=2\3
м)7,4\5,7 -9,1\11,4 =(74\10\57\10)-(91\10\114\10) =(74\10*10\57) -(91\10*10\114)=74\57 -91\114=74*2-91\114=57\114=1\2=0,5