По проекту для строительства нового 34 -х этажного здания на каждом с 3 го по 32 ой этажай предусмотрено установит 85 окон одинаковой конструкции. Сколько всего окон потребуется заказать для этих этажей?
Це завдання перевіряє вміння розв'язувати елементарні задачі з теми "Теорія ймовірностей".
1) Відомо, що формула ймовірності події має вигляд: , де A - подія; P(A) - ймовірність цієї події; n - кількість вcix можливих елементарних подій, а m - кількість елементарних подій, сприятливих А.
2) Думаємо так: - це ймовірність події витягнути одну ручку, нехай A - це ця подія, тоді .
3) Відомо, що олівців на 12 менше ніж ручок. Це означає, що якщо олівців є x (штук), то ручок тоді: x+12 (штук).
4) Захотівши один раз витягнути одну ручку, ви витягнете її, згідно умови, із олівців та всіх ручок, які є. Всього предметів у шухляді є лише ручки та олівці, тобто - це кількість усіх предметів у шухляді.
5) Що таке ймовірність події витягнути одну ручку? - Це відношення кількості усіх подій "витягування ручки із шухляди" до "кількості усіх подій". Події "витягування ручки із шухляди" - це ті події, які сприяють появі події витягування одної ручки, тобто появі події, ймовірність якої дорівнює . Тобто сприятливі події - це ті події, які задаються формулою x + 12
6) Знаючи, що ймовірність витягнути одну ручку дорівнює 5/8, тобто ; - це сприятливі події до події A (m), а - це кількість усіх подій (n), то складемо рівність опираючись на пункт 1 і знайдемо x, що і буде відповіддю на наше завдання:
Відповідь:
18 ОЛІВЦІВ.Покрокове роз'яснення:
Це завдання перевіряє вміння розв'язувати елементарні задачі з теми "Теорія ймовірностей".
1) Відомо, що формула ймовірності події має вигляд: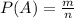 , де A - подія; P(A) - ймовірність цієї події; n - кількість вcix можливих елементарних подій, а m - кількість елементарних подій, сприятливих А.
, де A - подія; P(A) - ймовірність цієї події; n - кількість вcix можливих елементарних подій, а m - кількість елементарних подій, сприятливих А.
2) Думаємо так: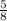 - це ймовірність події витягнути одну ручку, нехай A - це ця подія, тоді
- це ймовірність події витягнути одну ручку, нехай A - це ця подія, тоді 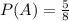 .
.
3) Відомо, що олівців на 12 менше ніж ручок. Це означає, що якщо олівців є x (штук), то ручок тоді: x+12 (штук).
4) Захотівши один раз витягнути одну ручку, ви витягнете її, згідно умови, із олівців та всіх ручок, які є. Всього предметів у шухляді є лише ручки та олівці, тобто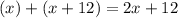 - це кількість усіх предметів у шухляді.
- це кількість усіх предметів у шухляді.
5) Що таке ймовірність події витягнути одну ручку? - Це відношення кількості усіх подій "витягування ручки із шухляди" до "кількості усіх подій". Події "витягування ручки із шухляди" - це ті події, які сприяють появі події витягування одної ручки, тобто появі події, ймовірність якої дорівнює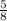 . Тобто сприятливі події - це ті події, які задаються формулою x + 12
. Тобто сприятливі події - це ті події, які задаються формулою x + 12
6) Знаючи, що ймовірність витягнути одну ручку дорівнює 5/8, тобто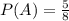 ;
; 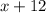 - це сприятливі події до події A (m), а
- це сприятливі події до події A (m), а 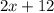 - це кількість усіх подій (n), то складемо рівність опираючись на пункт 1 і знайдемо x, що і буде відповіддю на наше завдання:
- це кількість усіх подій (n), то складемо рівність опираючись на пункт 1 і знайдемо x, що і буде відповіддю на наше завдання:
Тобто олівців у шухляді всього рівно 18.
(Гуманітарій - не оправдання)
1. В основании призмы лежат - многоугольники.
2. Боковые рёбра призмы - перпендикулярны основаниям.
3. Призма имеет 30 граней. В её основании лежит (какой многоугольник) - многоугольник в 28 углов, 84 рёбер, 56 вершин.
(Боковых граней 30-2=28. Значит это 28-угольник. Вершины = 28×2, рёбра = 28×2+28)
4. Диагональю призмы называется - отрезок, концами которого служат две вершины призмы, не лежащие на одной ее грани.
5. Прямоугольным параллелепипедом называется - прямая призма, основанием которой является прямоугольник.
6. Призма называется наклонной, если - ее боковые ребра не перпендикулярны основаниям.
7. Призма называется правильной, если - основанием которой является правильный многоугольник.
8. Площадью полной поверхности призмы называется сумма - всех боковых граней призмы.
9. Все двугранные углы при боковых гранях прямой призмы - прямые.
10. Площадь боковой поверхности куба с ребром 10 см равна - 600 см².
( так как у куба 4 боковых стороны и 2 основания, т.е. всего 6 квадратных сторон. А площадь одной стороны считается по формуле:
S = a², где а - длина стороны квадрата.
S = 10×10 = 100 см². - площадь одной стороны квадрата.
Тогда площадь всей поверхности куба:
S куба = 6×S
S куба = 6×100 = 600 см²).
11. Площадь полной поверхности куба с ребром 6 см равна - 216.
(так как грани куба - квадраты, площадь каждого квадрата равна
6² = 36. Куб состоит из шести таких квадратов значит площадь полной поверхности равна 36×6 = 216).
12. Площадь боковой поверхности правильной четырёхугольной призмы с высотой h и стороной основания a равна - Sб.п.= 4ah
13. Если диагональ куба равна d, то площадь полной поверхности куба равна - 2d²
(Так как S полy. пов. куба равна 6a² (а - ребро куба) ,
квадрат диагонали равен сумме квадратов всех измерений, тогда:
d²=3a² , тогда:
Sп.п. = 6a² = 2×(3a²) = 2d² )
14. Прямоугольный параллелепипед имеет три измерения, равные a=5 см, b=8 см, h =10 см. Площадь его полной поверхности равна - 340 см²
(Так как Sполн.пов. = Sбок. + 2Sосн.
Sбок. = Pосн. ×, S = 2×(5 + 8)×10 = 260 см²
Sосн. = а×в, S = 5×8 = 40 см²
Sполн. = 260 + 2×40 = 340 см²)
15.Площадь полной поверхности правильной треугольной призмы со стороной основания а и боковым ребром с равна - a²×√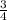 ×c = a²×c×√
×c = a²×c×√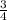
( Так как площадь основания равностороннего треугольника со стороной а = Sосн.= a²×√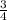
Таких оснований у призмы две.
Sбок.грани прямоугольника=
Sбок.гр. = a×c, таких граней три.
Sполн.пов. =
Sп.п. = 2×Sосн.+ 3×Sбок.гр. = a²×√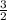 + 3ac
+ 3ac
Объем призмы =
V = Sосн.×H = a²×√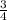 ×c = a²×c×√
×c = a²×c×√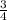 ).
).