Тебе нужен трудовой кодекс, посмотри статьи про выход на работу в выходные и праздничные дни, там всё найдёшь. это тк р казахстан статья 98 трудового кодекса предусматривает право работодателя привлечь работников к работе в выходные и праздничные дни независимо от согласия работников только в следующих исключительных случаях: для предотвращения чрезвычайных ситуаций, стихийного бедствия или производственной аварии либо немедленного устранения их последствий; для предотвращения и расследования несчастных случаев, гибели или порчи имущества; для выполнения неотложных, заранее непредвиденных работ, от выполнения которых зависит в дальнейшем нормальная работа организации в целом или ее отдельных подразделений
Пусть сумма кредита равна S, а годовые составляют а %. Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент: b = 1 + 0,01a. После первой выплаты сумма долга составит: S1 = Sb − X. После второй выплаты сумма долга составит: S2 = S1b − X = (Sb − X)b − X = Sb² − (1 + b)X. После третьей выплаты сумма оставшегося долга равна: S3 = Sb³ - (1-b+b²)X = Sb³ - · X После четвертой выплаты сумма оставшегося долга равна: S4 = - (1 + b +b² + b³)X = - · X По условию четырьмя выплатами Алексей должен погасить кредит полностью, поэтому - · X = 0. Потом выражаешь из этого выражения X и при S = 6902000 и а = 12,5, получаем: b = 1,125 получается: X = рублей
Пусть сумма кредита равна S, а годовые составляют а %. Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент: b = 1 + 0,01a.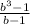 · X
· X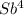 - (1 + b +b² + b³)X =
- (1 + b +b² + b³)X = 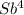 -
- 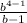 · X
· X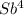 -
- 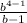 · X = 0.
· X = 0.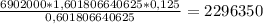 рублей
рублей
После первой выплаты сумма долга составит:
S1 = Sb − X.
После второй выплаты сумма долга составит:
S2 = S1b − X = (Sb − X)b − X = Sb² − (1 + b)X.
После третьей выплаты сумма оставшегося долга равна:
S3 = Sb³ - (1-b+b²)X = Sb³ -
После четвертой выплаты сумма оставшегося долга равна:
S4 =
По условию четырьмя выплатами Алексей должен погасить кредит полностью, поэтому
Потом выражаешь из этого выражения X и при S = 6902000 и а = 12,5, получаем: b = 1,125 получается:
X =