При каждом броске симметричной монеты возможны два исхода - {выпал орел} и {выпала решка}. Так как монета была подброшена раза, то всего исходов может быть (количество исходов при каждом броске независимо, поэтому двойки перемножаются).
Нам подходят всего лишь четыре исхода (О - орел, Р - решка): ОООР, ООРО, ОРОО и РООО (если без перебора в четыре случая, то исхода).
Так как при равновозможных элементарных исходах вероятность - это отношение числа благоприятных исходов ко всем исходом, то:
P = {число исходов, в которых выпало ровно три орла} / {число всех возможных исходов} = 4 / 16 = 1 / 4 = 0,25.
Симметричность в условии означает, что вероятность выпадения орла = P(орла) = Р(о) равна вероятности выпадения решки = P(решки) = Р(р). А так как две эти вероятности составляют полную группу событий (считаем, что в результате каждого броска возможен лишь один из этих двух исходов), т.е. P(o) + P(р) = 1, то, используя полученное выше равенство получаем : P(o) + P(0) = 1 => Р(о) = Р(р) = 0.5 или 50 процентов.
Т.к. броски монеты события независимые, то итоговая вероятность есть произведение вероятностей на каждом из них.
При каждом броске симметричной монеты возможны два исхода - {выпал орел} и {выпала решка}. Так как монета была подброшена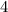 раза, то всего исходов может быть
раза, то всего исходов может быть 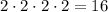 (количество исходов при каждом броске независимо, поэтому двойки перемножаются).
(количество исходов при каждом броске независимо, поэтому двойки перемножаются).
Нам подходят всего лишь четыре исхода (О - орел, Р - решка): ОООР, ООРО, ОРОО и РООО (если без перебора в четыре случая, то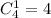 исхода).
исхода).
Так как при равновозможных элементарных исходах вероятность - это отношение числа благоприятных исходов ко всем исходом, то:
P = {число исходов, в которых выпало ровно три орла} / {число всех возможных исходов} = 4 / 16 = 1 / 4 = 0,25.
Задача решена!
ответ: 0,25 .А так как две эти вероятности составляют полную группу событий (считаем, что в результате каждого броска возможен лишь один из этих двух исходов), т.е. P(o) + P(р) = 1, то, используя полученное выше равенство получаем : P(o) + P(0) = 1 => Р(о) = Р(р) = 0.5 или 50 процентов.
Т.к. броски монеты события независимые, то итоговая вероятность есть произведение вероятностей на каждом из них.
P(выпадения орла 4 раза) = Р(о) * Р(о) * Р(о) * Р(о) = Р(о)^4 = 0.5 ^ 4 =
= 0.0625 = 6.25 процента