Заметим, что поскольку есть пара красных чисел с суммой 1 + 2011 = 2012, то число 2012 - 11 = 2001 - красное, иначе была бы пара синих чисел с суммой 11 + 2001 = 2012.
Теперь есть еще и красная пара с суммой 1 + 2001 = 2002, тогда 2002 - 11 = 1991 - тоже красное.
Аналогично, появилась пара красных чисел с суммой 1992, тогда и 1992 - 11 = 1981 обязано быть красным.
Повторив указанный выше процесс ещё 178 раз, получим, что число 201 - красное.
Повторяем написанное выше, но уже с синим числом 20. 1 и 201 - красные, тогда 202 - 20 = 182 - красное. Дальше находим, что красными будут и 1 + 182 - 20 = 163, 144, 125, 106, 87, 68, 49, 30 и 11
Исходя из рассуждения 11 должно быть красным, хотя по условию оно синее. Противоречие, исходное предположение неверно, и такие пары чисел найдутся.
ответ: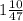
Решение: b/a=5/13;→13b=5a; b=5а/13
1)4а²+3ab-b²= 4а²-b² +3ab=(2a-b)(2a+b) +3ab
подставим вместо b зачение 5а/13
(2а- 5а/13)(2а+ 5а/13)+3а*5а/13=((26а-5а)/13)((26а+5а)/13) - 15а²/13=
=21а*31 а/13*13- 13*15а²/13²=651а²/13²-195а²/13²=456а²/13²
2)4a-5ab+b²=(2a)²-4ab+ b² -ab=(2a-b)²-ab
подставим вместо b зачение 5а/13
(2а- 5а/13)²- 5а²/13=((26а-5а)/13)²- 13*5а²/13²=21²а²/13²-65а²/13=376а²/13²
3)поделим 1) на 2)
456а²/13²:376а²/13²=456а²/13²* 13²/376а²= ( 13²и а² сокращаем)=456/376=(сокращаем на 8)=57/47=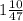
Пусть таких чисел не нашлось.
Заметим, что поскольку есть пара красных чисел с суммой 1 + 2011 = 2012, то число 2012 - 11 = 2001 - красное, иначе была бы пара синих чисел с суммой 11 + 2001 = 2012.
Теперь есть еще и красная пара с суммой 1 + 2001 = 2002, тогда 2002 - 11 = 1991 - тоже красное.
Аналогично, появилась пара красных чисел с суммой 1992, тогда и 1992 - 11 = 1981 обязано быть красным.
Повторив указанный выше процесс ещё 178 раз, получим, что число 201 - красное.
Повторяем написанное выше, но уже с синим числом 20. 1 и 201 - красные, тогда 202 - 20 = 182 - красное. Дальше находим, что красными будут и 1 + 182 - 20 = 163, 144, 125, 106, 87, 68, 49, 30 и 11
Исходя из рассуждения 11 должно быть красным, хотя по условию оно синее. Противоречие, исходное предположение неверно, и такие пары чисел найдутся.