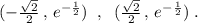Войти Регистрация Спроси ai-bota

Подробное решение найдите точки перегиба функции f(x) = $e^{-x^{2}}$

Показать ответ

Ответ:

Aron91

10.10.2020 00:36

$f(x)=e^{-x^2}\\\\f'(x)=e^{-x^2}\cdot (-2x)=-2x\cdot e^{-x^2}\\\\f''(x)=-2\cdot e^{-x^2}-2x\cdot (-2x\cdot e^{-x^2})=4\cdot e^{-x^2}\cdot (-\frac{1}{2}+x^2)=0\\\\4e^{-x^2}\cdot (x-\frac{1}{\sqrt2})\cdot (x+\frac{1}{\sqrt2})=0\\\\e^{-x^2}0\; \; \to \; \; x=\pm \frac{1}{\sqrt2}=\pm \frac{\sqrt2}{2}\\\\znaki:\; \; +++(-\frac{\sqrt2}{2})---(\frac{\sqrt2}{2})+++$

Точки перегиба: $(-\frac{\sqrt2}{2}\, ,\, e^{-\frac{1}{2}})\; \; ,\; \; (\frac{\sqrt2}{2}\, ,\, e^{-\frac{1}{2}})\; .$

0,0(0 оценок)

Популярные вопросы: Математика

gfjew56df

17.02.2023 08:33

Вынесите у (игрек) -0,5 ln |-2y+3| -x=c...

AknelaYouTuber

24.04.2021 18:07

Из точки плоскости проведены 2 равные наклонные длино 10м. Угол между наклонными 60 градусов. Найти расстояние от этой точки до плоскости если проекции наклонные перпендикулярны...

ваня10001

29.07.2021 17:07

Художник нарисовал 24 иллюстрации что составило три пятых всех иллюстраций книги сколько иллюстраций ему осталось нарисовать...

arsenijakula

16.12.2022 15:55

С Р О Ч Н О! С Р О Ч Н О! С Р О Ч Н О! 1 доллар стоит 2,72 монеты. Кроме того, за каждый покупаемый или продаваемый один доллар потребитель дополнительно уплачивает 2...

komikadza

28.10.2022 08:30

скорость катера по течению 18,7 км/ч а собственная скорость катера 16,5 км/ч найдите скорость катера против течения...

aibek6707

26.06.2022 02:44

Выполните действие8,2×(-5,7)...

375196albert

01.07.2022 04:24

. 110 . x = 9900 у . 78 = 19 734 1800:z=45u:216=14750*(v-173)=25001748:w+77=123...

0000094

18.07.2021 15:51

Нужен морфологический разбор слов ,,Зелёная(травка)...

Nikitaue

27.11.2020 05:08

На празднике собралось 7 семейных пар. Каждый мужчина при встрече руки всем, кроме собственной жены. Женщины друг другу руки не пожимали. Сколько было рукопожатий?...

wwwraisakravets

18.03.2023 11:36

в пяти ящиках лежат красные синие и белые шары число синих шаров в каждом ящике равно общему числу белых шаров во всех остальных ящиках а число белых шаров в каждом ящике...

Полный доступ

Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota Оформи подписку