Числа 500000000 и 13 (простое число) взаимно простые, поэтому дробь
является несократимой.
Применим следующую теорему о длине периода:
Если натуральное число m не делится на 2 и на 5, то период десятичной дроби, равной несократимой простой дроби n/m, начинается сразу после запятой. Его длина равна наименьшему d, при котором число, составленное из d девяток делится на m.
Рассмотрим числа составленные только из цифры 9:
9=3² не делится на 13;
99=3²·11¹ не делится на 13;
999=3³·37¹ не делится на 13;
9999=3²·11¹·101¹ не делится на 13;
99999=3²·41¹·271¹ не делится на 13;
999999=3³·7¹·11¹·13¹·37¹ делится на 13, тогда длина периода равна 6!
Так как дробь можно записать в виде:
то длина несократимой простой дроби равна 6. Отсюда:
В силу этого можно ответить поставленным вопросам:
3846153...: Какой будет следующая цифра в частном? 8, так как после 3 следует всегда 8.
3846153...: Сколько ещё цифр в частном можно записать, не выполняя деление? одну, так как умножается на 100000000=10⁸, а число 3846153 уже состоит из 7 цифр.
На кухне мальчики сидят на трёхногих табуретках, а девочки на четырёхногих. Всего на кухне 50 ног (считаются ноги детей и табуреток). Сколько в комнате мальчиков, если девочек не менее одной?
Пусть мальчиков m, а девочек d. Тогда:
(3+2)*m+(4+2)*d=50
5m+6d=50
Так как 5m и 50 делится на 5, то и 6d должно делиться на 5. Это выполняется только тогда, когда d делится на 5.
Так как d>0, то проверку начинаем с d=5:
d=5: 5m+6*5=50; 5m+30=50; 5m=20; m=4
d=10: 5m+6*10=50; 5m+60=50; 5m=-10; m=-2 - отрицательное число мальчиков быть не может
8
одну
Пошаговое объяснение:
Числа 500000000 и 13 (простое число) взаимно простые, поэтому дробь
является несократимой.
Применим следующую теорему о длине периода:
Если натуральное число m не делится на 2 и на 5, то период десятичной дроби, равной несократимой простой дроби n/m, начинается сразу после запятой. Его длина равна наименьшему d, при котором число, составленное из d девяток делится на m.
Рассмотрим числа составленные только из цифры 9:
9=3² не делится на 13;
99=3²·11¹ не делится на 13;
999=3³·37¹ не делится на 13;
9999=3²·11¹·101¹ не делится на 13;
99999=3²·41¹·271¹ не делится на 13;
999999=3³·7¹·11¹·13¹·37¹ делится на 13, тогда длина периода равна 6!
Так как дробь можно записать в виде:
то длина несократимой простой дроби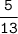
равна 6. Отсюда:
В силу этого можно ответить поставленным вопросам:
3846153...: Какой будет следующая цифра в частном? 8, так как после 3 следует всегда 8.
3846153...: Сколько ещё цифр в частном можно записать, не выполняя деление? одну, так как умножается на 100000000=10⁸, а число 3846153 уже состоит из 7 цифр.
4/Задание № 6:
На кухне мальчики сидят на трёхногих табуретках, а девочки на четырёхногих. Всего на кухне 50 ног (считаются ноги детей и табуреток). Сколько в комнате мальчиков, если девочек не менее одной?
Пусть мальчиков m, а девочек d. Тогда:
(3+2)*m+(4+2)*d=50
5m+6d=50
Так как 5m и 50 делится на 5, то и 6d должно делиться на 5. Это выполняется только тогда, когда d делится на 5.
Так как d>0, то проверку начинаем с d=5:
d=5: 5m+6*5=50; 5m+30=50; 5m=20; m=4
d=10: 5m+6*10=50; 5m+60=50; 5m=-10; m=-2 - отрицательное число мальчиков быть не может
ОТВЕТ: 4 мальчика