Математика: Покажите, что векторы a, b, c компланарны, если c=3a-7b

Покажите, что векторы a, b, c компланарны, если c=3a-7b

Показать ответ

Ответ:

papa63428

24.06.2022 03:46

Пояснение:

Сравнение чисел.

• Положительные числа.

При сравнении положительных чисел больше то, у которого больше модуль (само число). Положительные числа всегда больше "0" (нуля).

• Отрицательные числа.

При сравнении отрицательных чисел больше то, у которого меньше модуль (само число). Отрицательные числа всегда меньше "0" (нуля).

• Положительные числа всегда больше отрицательных.

Модуль - расстояние на координатной прямой от нуля до некой точки.

Модуль всегда равняется положительному числу, (НЕ МОЖЕТ РАВНЯТЬСЯ ОТРИЦАТЕЛЬНОМУ ЧИСЛУ! т.к. по сути это расстояние), т.е. модуль положительного числа равен положительному числу, а модуль отрицательного числа тоже равен положительному числу.

Например, |12| = 12; |- 64| = 64; и т.д.

Решение / ответ:

• 15 ✓ - 33,12;

15 > - 33,12.

• - 15 ✓ - 19;

- 15 > - 19.

• - 33 ✓ 0;

- 33 < 0.

• - 5,5 ✓ 5,05;

- 5,5 < 5,05.

• 1,001 ✓ 0;

1,001 > 0.

• - 18,02 ✓ - 18,03;

- 18,02 > - 18,03.

• 333 ✓ 555;

333 < 555.

Удачи Вам! :)

0,0(0 оценок)

Ответ:

elena30lazarev

02.05.2022 16:16

$\beta\in[0;1]:\\ \alpha\geq 0: \lim\limits_{n\to\infty}\sqrt[n]{\dfrac{\alpha^n}{\beta^n+n}}=\lim\limits_{n\to\infty}\sqrt[n]{\dfrac{\alpha^n}{n}}=\alpha$

Тогда, по признаку Коши, при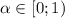 $\alpha\in[0;1)$ ряд сходится, при 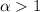$\alpha 1$ расходится.

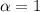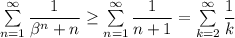При $\alpha=1$ имеем $\sum\limits_{n=1}^\infty\dfrac{1}{\beta^n+n}\geq \sum\limits_{n=1}^\infty\dfrac{1}{n+1}= \sum\limits_{k=2}^\infty\dfrac{1}{k}$ Гармонический ряд расходится, а тогда исходный ряд расходится по признаку сравнения.

$\alpha$

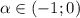При $\alpha\in(-1;0)$ ряд сходится, т.к. ряд из модулей (по доказанному выше) сходится.

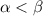$\alpha\lim\limits_{n\to\infty}{|\dfrac{\alpha^n}{\beta^n+n}|}=\lim\limits_{n\to\infty}{\dfrac{|\alpha|^n}{n}}=+\infty$ необходимое условие не выполнено, а значит ряд расходится.

$\alpha=-1= a_{n+1}$ , а тогда по признаку Лейбница ряд сходится.

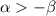$\beta1:\\ \alpha\geq 0: \lim\limits_{n\to\infty}\sqrt[n]{\dfrac{\alpha^n}{\beta^n+n}}=\lim\limits_{n\to\infty}\sqrt[n]{\dfrac{\alpha^n}{\beta^n}}=\dfrac{\alpha}{\beta}$

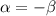Тогда при $\alpha$ ряд сходится, при $\alpha\beta$ расходится.

$\alpha=\beta=\lim\limits_{n\to\infty}{\dfrac{\beta^n}{\beta^n+n}}=1$ - необходимое условие не выполнено, ряд расходится.

$\alpha$

Тогда при $\alpha-\beta$ ряд сходится.

При $\alpha=-\beta$ необходимое условие не выполнено, ряд расходится.

$\alpha|\alpha|=-\alpha\beta\\=\lim\limits_{n\to\infty}{|\dfrac{\alpha^n}{\beta^n+n}|}=\lim\limits_{n\to\infty}{\dfrac{|\alpha|^n}{\beta^n}}=+\infty$ необходимое условие не выполнено, ряд расходится.