Покажите решениеmnpk сторона mn y см выразите остальные стороны этого четырёхугольника если np на 4 см меньше мn pk в3.5 раза больше рк​

Пошаговое объяснение:

Ну, перво -наперво нужно увидеть, какой график нам дан, в Вашем случае - это график производной ф-ции y = f'(x)

Когда мы ищем точки максимума и минимума (экстремумы ф-ции, xmax, xmin), то должно выполняться условие: f'(x) = 0

Ф-ция возрастает, когда f'(x) > 0,

убывает, когда f'(x) < 0

Максимальные значения ф-ция принимает при подстановке в ф-цию xmax, т.е. fmax (xmax)

Минимальное значения ф-ция принимает при подстановке в ф-цию xmin, т.е. fmin (xmin)

В Вашем случае f'(x) > 0 при х < 2 - т.е. возрастала

f'(x) < 0 при х > 2, точка х = 2 - точка максимума (образуется "горка")

f'(x)       +                -

2

         /                     \

точка х = -2 - это так называемая точка перегиба, но ни в коем случае не экстремум, т.к. ф-ция все равно продолжала возрастать.

ответ: только одна точка, х = 2

Правильная четырёхугольная пирамида.

FG = 6 (см).

FH = 10 (см).

AB = ? (см).

В основании правильной четырёхугольной пирамиды лежит квадрат, поэтому все стороны в основании будут равны.

Когда мы опустили высоту к основанию и провели апофему к боковой грани нашей пирамиды, то у нас образовался прямоугольный △FGH, где FH - гипотенуза прямоугольного треугольника (апофема пирамиды), GH - катет прямоугольного треугольника, FG - катет прямоугольного треугольника (высота пирамиды).

Мы сможем найти длину катета GH по теореме Пифагора (a = √(c² - b²), где a и b - катеты, c - гипотенуза).

(см).

Катет прямоугольного треугольника, который образован апофемой пирамиды, высотой и отрезком, их соединяющим, равен половине длины основания правильной четырёхугольной пирамиды.

Т.е. GH = HC = DH = 8 (см).

Так как апофема по свойству делит сторону основания пирамиды пополам, то:

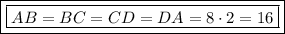(см).