Покидайте типа: на сколько % изменится число если к нему прибавить или уменьшить на сколько-то %,потом например вычти из него сколько-то %
и так примерно раза 3 сделать с числом
минимум 5 .
​

Группируем дроби по парам и выносим в каждой паре общий множитель:

Пошаговое объяснение:1/9×(1/7+1/11)+1/13×(1/11+1/15)+1/17×(1/15+1/19)+1/19×21=

Решение в прикрепленном файле. Если возникнут вопросы, обращайтесь.

1/9×((1 )/7 +1/11) +1/13 ×(1/11 + 1/15) +1/17×(1/15 +1/19) +1/(19×21) = 1/9×18/(7×11) +1/13×26/(11×15) +1/17×34/(15×19) +1/(19×21)=

Сокращаем 9 и 18; 26 и 13; 34 и 17 и  получим уже четыре дроби

2/(7×11) +2/(11×15) +2/(15×19) +1/(19×21) =   вновь группируем и выносим общие множители

1/11×(2/7+2/15) +1/19×(2/15+1/21) = дроби в скобках приводим к общему знаменателю и складываем

1/11×44/15 +1/19×57/(15×21)= опять сокращаем - 11 и 44; 19 и 57

4/(7×15) +3/(15×21)= и последний раз выносим общий множитель, дроби в скобках приводим к общему знаменателю, складываем и сокращаем получившийся результат-

1/15×(4/7+3/21) =  1/15×(4/7+1/7) = 1/15×5/7=1/3×1/7=  1/21  - ответ, который был получен ответ без громоздких вычислений.  

Второй пример решается аналогичным образом:

2/7×(1/3 +1/11)+2/15(1/11 +1/19) +2/23(1/19 + 1/27) = дроби в скобках приводим к общему знаменателю и складываем

2/7×14/(3×11) +2/15×30/(11×19) +2/23×46/(19×27) = сокращаем 7 и 14; 15 и 30;  23 и 46

(2×2)/(3×11) +(2×2)/(11×19) +(2×2)/(19×27) = вновь группируем и выносим общий множитель

4/11×(1/3 + 1/19) + 4/(19×27) = (4×22)/(11×3×19) + 4/(19×27) = сокращаем 11 и 22 и выносим общий множитель 4/19  

4/19×(2/3 +1/27) =(4×57)/(19×3×27) = сокращаем 19 и 57, получаем (4×3)/(3×27), сокращаем на 3 и получаем

ответ 4/27

ответ: смотри ниже там и решение и ответ

Пошаговое объяснение:

Задание 1

а)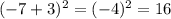

б)—7+3² = -7 + 9 = 2

в) (-7)² + 3² = 49+9 = 58

г) ((-2)⁴+(-1)³*7):(-3)² = (16+(-1*7)):9= (16-7):9 = 9:9 = 1

д) -0,5² -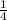 *(0,05:(-0,1)²-2¹) = -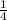-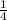*(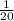:0,1²-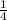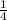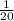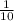2) = --*(:()²-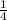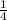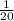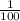2) =- - *(:-2) =

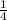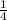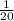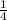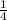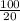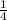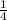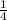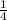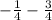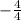- - * ( * 100 -2) = - - * (-2) = --(5-2)=--*3= = = -1

Задание 2

а) (а²)⁵ = а¹⁰

б) а⁹ * а³ = а¹²

в) а¹⁹*(а²)⁷ = а¹⁹ * а¹⁴ = а³³

г) (а⁴)²: (а²)³ = а⁸ : а⁶ = а²

д) (-2ab)³ = -8a³b³

e) (-0,1xy²z)⁵ = -0,00001x⁵y¹⁰z⁵

ж) (-(5/7)m³n⁴)²=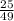 m⁶n⁸

Задание 3

a) 2x²y³ * (-4xy²) = -8x³y⁵

б) 0,5a(-b)⁶ *10a²b² = 5a³b⁸

в) 6⁻¹(-c)⁵ab³ *(-6cab³) = a²b⁶c⁶

Задание 4 здесь очень тяжело писать