Поле зорали за два дні. Першого дня було зорано 100 га, а другого – 150 га. Скільки відсотків усієї площі було зорано першого дня і скільки другого РЕШИТЬ
А)) 96-2= 94стр с цифрами 9-2=7 стр однозначных, цифр для них тоже 7. (3,4,5,6,7,8,9). 94-7= 87 стр остаётся 87•2= 174 цифры для двузначных номеров страниц (10,11,12...)
174+7= 181 цифра всего
ответ: для нумерации книги 96 страниц использовали 181 цифру.
Б)) 1200-2= 1198 стр пронумерованы
9-2=7 стр однозначных, и 7 цифр использовали
99-9= 90стр двузначных
90•2=180цифр для них Это (10,11,12...98,99)
1198-7-90= 1101 стр остались
999-99= 900 страниц с тремя цифрами 900•3=2700 цифр для них (100,101,102...998,999)
1101-900= 201 стр осталась их четырьмя цифрами пронумеровано
201•4= 804 цифры использовали
7+180+2700+804= 3691 цифра всего
ответ: для книги 1200 страниц использовали 3691 цифру
Первое уравнение системы задает окружность радиуса 3 с центром в точке (3,4)
Второе уравнение - смещенный на единицу вверх график модуля x, который можно двигать влево или вправо меняя значения параметра (смотрите чертеж в прикр. файлах)
Становится понятно, что при смещении вправо графика модуля наступит такой момент, при котором левая его ветвь будет касаться окружности... После этого момента, графики модуля и окружности будут иметь 4 точки пересечения. Продолжая двигаться вправо, придем к значению , которое, как несложно сообразить, соответствует трем точкам пересечения. Наконец, дойдем до такого значения параметра, при котором правая ветвь станет касательной к окружности, снова будет 3 общие точки. Таким образом надо найти при каких значениях параметра наши прямые/ветви являются касательными к окружности.
Из уравнения окружности выделим нижнюю часть, нам интересна только она, ибо только ее касаются прямые:
Затем найдем такой параметр, при котором уравнения:
и
имеют единственные решения. Они сводятся к квадратным:
и
Квадратные уравнения имеют единственное решение при нулевом дискриминанте (соответствует случаю касания графиков). Рассмотрим подробно второе выражение, первое делается аналогично. Его дискриминант:
Получили два значения параметра, лишь одно из них верное. Как выбрать? Т.к. параметр отвечает за смещение влево/вправо графика модуля относительно точки (0,1), то отрицательное значение сместит наш график (вершину угла образованного оранжевой ломаной на чертеже, если дословно) на отрицательную часть оси x, что, очевидно, совершенно неправильный случай.
Таким же образом находим из первого выражения
Итого получили всего 3 значения параметра при которых система имеет ровно три решения.
А)) 96-2= 94стр с цифрами
9-2=7 стр однозначных, цифр для них тоже 7. (3,4,5,6,7,8,9).
94-7= 87 стр остаётся
87•2= 174 цифры для двузначных номеров страниц (10,11,12...)
174+7= 181 цифра всего
ответ: для нумерации книги 96 страниц использовали 181 цифру.
Б)) 1200-2= 1198 стр пронумерованы
9-2=7 стр однозначных, и 7 цифр использовали
99-9= 90стр двузначных
90•2=180цифр для них
Это (10,11,12...98,99)
1198-7-90= 1101 стр остались
999-99= 900 страниц с тремя цифрами
900•3=2700 цифр для них
(100,101,102...998,999)
1101-900= 201 стр осталась их
четырьмя цифрами пронумеровано
201•4= 804 цифры использовали
7+180+2700+804= 3691 цифра всего
ответ: для книги 1200 страниц использовали 3691 цифру
Первое уравнение системы задает окружность радиуса 3 с центром в точке (3,4)
Второе уравнение - смещенный на единицу вверх график модуля x, который можно двигать влево или вправо меняя значения параметра (смотрите чертеж в прикр. файлах)
Становится понятно, что при смещении вправо графика модуля наступит такой момент, при котором левая его ветвь будет касаться окружности... После этого момента, графики модуля и окружности будут иметь 4 точки пересечения. Продолжая двигаться вправо, придем к значению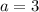 , которое, как несложно сообразить, соответствует трем точкам пересечения. Наконец, дойдем до такого значения параметра, при котором правая ветвь станет касательной к окружности, снова будет 3 общие точки. Таким образом надо найти при каких значениях параметра наши прямые/ветви являются касательными к окружности.
, которое, как несложно сообразить, соответствует трем точкам пересечения. Наконец, дойдем до такого значения параметра, при котором правая ветвь станет касательной к окружности, снова будет 3 общие точки. Таким образом надо найти при каких значениях параметра наши прямые/ветви являются касательными к окружности.
Из уравнения окружности выделим нижнюю часть, нам интересна только она, ибо только ее касаются прямые:
Затем найдем такой параметр, при котором уравнения:
и
имеют единственные решения. Они сводятся к квадратным:
и
Квадратные уравнения имеют единственное решение при нулевом дискриминанте (соответствует случаю касания графиков). Рассмотрим подробно второе выражение, первое делается аналогично. Его дискриминант:
Получили два значения параметра, лишь одно из них верное. Как выбрать? Т.к. параметр отвечает за смещение влево/вправо графика модуля относительно точки (0,1), то отрицательное значение сместит наш график (вершину угла образованного оранжевой ломаной на чертеже, если дословно) на отрицательную часть оси x, что, очевидно, совершенно неправильный случай.
Таким же образом находим из первого выражения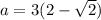
Итого получили всего 3 значения параметра при которых система имеет ровно три решения.