Положительные числа x и y таковы, что xy=50. Найдите наименьшее возможное значение выражения (x/2)+y. В этой задаче пришел к тому, что x*x+y*y( *-знак умножения) больше или равен 100. Это как подсказка. ответ дать с полным объяснением, а не просто сказать ответ!
Найдем минимум выражения в скобках. Заметим что положительный x можно представить в виде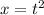
Отметим, что получившееся выражение не может быть меньше 20, а значение 20 достигается при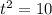 то есть при
то есть при 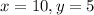
И минимальное значение исходного выражения составляет 10/2 + 5 = 10