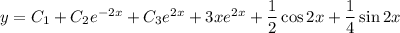— неоднородное дифференциальное уравнение третьего порядка с постоянными коэффициентами
Принцип суперпозиции решений
Общее решение такого уравнения: , где — общее решение соответствующего однородного уравнения, — частное решение неоднородного дифференциального уравнения с постоянными коэффициентами.
Метод Эйлера:
Характеристическое уравнение:
Фундаментальная система решений:
Общее решение:
Здесь
Контрольные числа: — является корнем характеристического уравнения; — не является корнем характеристического уравнения;
Тогда и
Находим неизвестные коэффициенты методом неопределенных коэффициентов:
наименьшее значение функции на отрезке [-3; 0] равно 2
Пошаговое объяснение:
найдем критические точки функции и посмотрим на условие непрерывности функции
для этого найдем производную
функция существует и непрерывна везде и в том числе на отрезке [-3; 0], значит по теореме Вейерштрасса, на отрезке функция имеет точки экстремума.
найдем критические точки функции
6x² - 6x -36 =0
6(x²- x -6) = 6(x-3)(x+2)
точки х = 2, х = -3
точка х=2 не принадлежит нашему отрезку, она нас не интересует
найдем значения функции в критической т х= -3 и на конце отрезка х=0
f(0) = 2
f(-3) = 29
наименьшее значение функции на отрезке [-3; 0] равно 2
Принцип суперпозиции решений
Общее решение такого уравнения: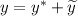 , где
, где 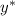 — общее решение соответствующего однородного уравнения,
— общее решение соответствующего однородного уравнения, 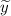 — частное решение неоднородного дифференциального уравнения с постоянными коэффициентами.
— частное решение неоднородного дифференциального уравнения с постоянными коэффициентами.
Метод Эйлера: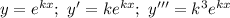
Характеристическое уравнение: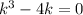
Фундаментальная система решений:
Общее решение: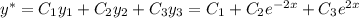
Здесь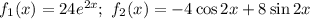
Контрольные числа: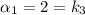 — является корнем характеристического уравнения;
— является корнем характеристического уравнения; 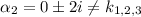 — не является корнем характеристического уравнения;
— не является корнем характеристического уравнения;
Тогда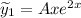 и
и 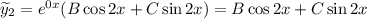
Находим неизвестные коэффициенты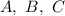 методом неопределенных коэффициентов:
методом неопределенных коэффициентов:
Коэффициенты около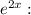
Коэффициенты около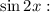
Коэффициенты около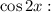
Таким образом,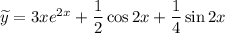
Общее решение заданного уравнения:
ответ: