Пользуясь правилами вычисления производных, найдите .

Задание 1 

Пусть х - работает первый насос, у - работает второй насос  (производительность в минуту) , а Р - вся работа.

Р/(х+у)=20мин

Р/х=30

Из Р/х=30 найдем Х

х=Р/30

Подставим в первое уравнение:

Р/(Р/30+у)=20

Р=20*(Р/30+у)

Р=2/3Р+20у

20у=Р/3

у=Р/60 - это означает что производительность насоса равна вся работа деленная на 60 минут, то есть потребуется 60 мин , чтобы второй насос перекачал нефть

ответ. 60 минут

Задание 2

( 7,85х - 12,4х ) * (-1 9/91) = - 2 11/12 - 1 2/3

-4.55х* (- ) =  -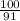 

= 

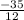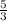
5x=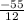 

x=  *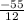 

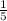
x=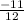 

240*1/3=80 рублей потратили на первую покупку

240-80=160р

160*3/4=120 рублей потратили на вторую покупку

160-120=40 рублей осталось

ответ: 40 рублей

7. Для удобства вычислений будем считать, что объём бассейна равен 1.

Тогда скорость, с которой бассейн наполняет первая труба, будет равна 1/ 45, а скорость, с которой бассейн наполняет вторая труба, будет, соответственно, равна 1/30.

Значит, две трубы вместе будут наполнять бассейн со скоростью:

1/30 + 1/45 = 3/90 + 2/90 = 5/90 = 1/18.

Следовательно, бассейн наполнится водой за

1 : 1/18 = 1 * 18 = 18 (минут).

ответ: 18 минут.