x1 = 8 м/с и x2 = 10 м/с - в момент времени t1 = 1
x1 = 24 м/с и x2 = 22 м/с в момент времени t2 = 3
Пошаговое объяснение:
Указанные законы
описывают функциональные зависимости расстояния х1 и х2 от времент t
Моментами, когда пройденные точками расстояния равны, будут такие моменты времени t, при которых
будет соблюдаться равенство:
Скорости точек v1 ,v2 определяются как производные от функций расстояния в заданные моменты времени t,
1. Определим моменты времени t, когда выполняется равенство
Решим уравнение
По Т. Виета разбиваем на множители:
2. Найдем скорости точек в моменты времени t1 и t2
2а) Определим формулы скорости:
2б) Найдем скорости точек в моменты времени t1 и t2
Площадь квадрата:
S₁ = a² (м²)
Площадь двух кругов:
S₂ = 2πa²/4 = πa²/2 (м²)
Тогда:
S = S₁+S₂ = a² + πa²/2
1000 = a² + 1,5a²
2,5a² = 1000
a² = 400
a = 20 (м) - длина стороны квадрата
R = a/2 = 20:2 = 10 (м) - радиус кругов
Длина забора: L = 2*2πR = 4*3*10 = 120 (м)
Пошаговое объяснение ПОСТАВЬ ЛАЙК
x1 = 8 м/с и x2 = 10 м/с - в момент времени t1 = 1
x1 = 24 м/с и x2 = 22 м/с в момент времени t2 = 3
Пошаговое объяснение:
Указанные законы
описывают функциональные зависимости расстояния х1 и х2 от времент t
Моментами, когда пройденные точками расстояния равны, будут такие моменты времени t, при которых
будет соблюдаться равенство:
Скорости точек v1 ,v2 определяются как производные от функций расстояния в заданные моменты времени t,
1. Определим моменты времени t, когда выполняется равенство
Решим уравнение
По Т. Виета разбиваем на множители:
2. Найдем скорости точек в моменты времени t1 и t2
2а) Определим формулы скорости:
2б) Найдем скорости точек в моменты времени t1 и t2
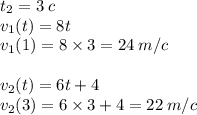
8 м/с и 10 м/с в момент времени t1 = 124 м/с и 22 м/с в момент времени t2 = 3Площадь квадрата:
S₁ = a² (м²)
Площадь двух кругов:
S₂ = 2πa²/4 = πa²/2 (м²)
Тогда:
S = S₁+S₂ = a² + πa²/2
1000 = a² + 1,5a²
2,5a² = 1000
a² = 400
a = 20 (м) - длина стороны квадрата
R = a/2 = 20:2 = 10 (м) - радиус кругов
Длина забора: L = 2*2πR = 4*3*10 = 120 (м)
Пошаговое объяснение ПОСТАВЬ ЛАЙК