Обыкновенные дроби, определение и примеры
Обыкновенные дробиприменяются для описания количества долей. Рассмотрим пример, который приблизит нас к определению обыкновенной дроби.
Представим апельсин, состоящий из
12
долек. Каждая доля тогда будет – одна двенадцатая или
1
/
. Две доли –
2
; три доли –
3
и т.д. Все
долей или целое число будет выглядеть так:
. Каждая из используемых в примере записей является примером обыкновенной дроби.
Определение 3
Обыкновенная дробь – это запись вида
m
n
или
, где
и
являются любыми натуральными числами.
Согласно данному определению, примерами обыкновенных дробей могут быть записи:
4
9
,
11
34
917
54
. А такие записи:
√
5
не являются обыкновенными дробями.
Пошаговое объяснение:
SΔABC = 3 * AD = 3Q
1) Рассмотрим ΔCMB:
Scmb = Samc (т.к. основание - равносторонний треугольник, то MA = MC = MB ⇒ площади граней равны) = Q
Scmb = = = Q (a - сторона ΔABC)
2) Рассмотрим ΔOMD:
Так как ∠ODM = 60°, то ∠OMD = 30° ⇒ OD = MD (сторона, лежащая против угла 30° равна половине гипотенузы)
3) Так как ΔABC равносторонний, то все высоты пересекаются в одной точке и делятся ей в отношении 1:2 (OD = AD)
4) SΔ = a * h ⇒ SΔABC = a * AD
Q = * MD; MD = 2*OD; OD = AD ⇒ Q = * AD = AD
Обыкновенные дроби, определение и примеры
Обыкновенные дробиприменяются для описания количества долей. Рассмотрим пример, который приблизит нас к определению обыкновенной дроби.
Представим апельсин, состоящий из
12
долек. Каждая доля тогда будет – одна двенадцатая или
1
/
12
. Две доли –
2
/
12
; три доли –
3
/
12
и т.д. Все
12
долей или целое число будет выглядеть так:
12
/
12
. Каждая из используемых в примере записей является примером обыкновенной дроби.
Определение 3
Обыкновенная дробь – это запись вида
m
n
или
m
/
n
, где
m
и
n
являются любыми натуральными числами.
Согласно данному определению, примерами обыкновенных дробей могут быть записи:
4
/
9
,
11
34
,
917
54
. А такие записи:
√
11
5
,
1
,
9
4
,
3
не являются обыкновенными дробями.
Пошаговое объяснение:
SΔABC = 3 *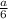
AD = 3Q
Пошаговое объяснение:
1) Рассмотрим ΔCMB:
Scmb = Samc (т.к. основание - равносторонний треугольник, то MA = MC = MB ⇒ площади граней равны) = Q
Scmb =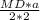
= 
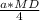= Q (a - сторона ΔABC)
2) Рассмотрим ΔOMD:
Так как ∠ODM = 60°, то ∠OMD = 30° ⇒ OD =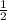
MD (сторона, лежащая против угла 30° равна половине гипотенузы)
3) Так как ΔABC равносторонний, то все высоты пересекаются в одной точке и делятся ей в отношении 1:2 (OD =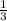
AD)
4) SΔ =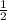
a * h ⇒ SΔABC = 
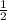a * AD
Q =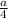
* MD; MD = 2*OD; OD = 
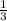AD ⇒ Q = 
* 
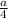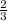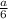AD = 
AD
SΔABC = 3 *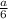
AD = 3Q