1.Найдите косинус угла между векторами а и б,если а(0;-4) б(20;-15)
2.Вычислите: вектор а минус ветор б,если вектор а=вектору б=1 и угол вектора а и б=45 граусов.
3.Докажите,что векторы ВА и ВС перпендикулярны,если А(0;1) В(2;3) С(-1;6) Попроси больше объяснений Следить Отметить нарушение Banalnoyes 27.01.2013 Реклама
ответы и объяснения
Участник Знаний
1)Косинус угла между векторами, зная их координаты вычисляется по формуле:
cos α = \frac{x_{1}x_{2} + y_{1}y_{2}}{\sqrt{x_{1}^2 + y_{1}^2}\sqrt{x_{2}^2 + y_{2}^2} } Здесь x1,x2, y1, y2 - координаты двух векторов. Подставив в эту формулу координаты, получим:
2.Вычислите: вектор а минус ветор б,если вектор а=вектору б=1 и угол вектора а и б=45 граусов.
3.Докажите,что векторы ВА и ВС перпендикулярны,если А(0;1) В(2;3) С(-1;6)
Попроси больше объяснений Следить Отметить нарушение Banalnoyes 27.01.2013
Реклама
ответы и объяснения
Участник Знаний
1)Косинус угла между векторами, зная их координаты вычисляется по формуле:
cos α = \frac{x_{1}x_{2} + y_{1}y_{2}}{\sqrt{x_{1}^2 + y_{1}^2}\sqrt{x_{2}^2 + y_{2}^2} }
Здесь x1,x2, y1, y2 - координаты двух векторов.
Подставив в эту формулу координаты, получим:
cos α = (0 * 20 + 60) / √16 * √(20² + (-15)²) = 60 / 4 * √625 = 60 / 4 * 25 = 60/100 = 0.6
1. Дополнительное построение: высота BH (смотреть в приложении).
2. Так как AB = BC = 13, то треугольник ABC - равнобедренный (по признаку).
3. Так как BH - высота, то треугольник ABH - прямоугольный.
4. Так как BH - высота и треугольник ABC - равнобедренный, то BH - медиана (по свойству равнобедренного треугольника).
5. Так как BH - медиана, то AH = HC = 5 (так как медиана делит сторону пополам).
6. Так как треугольник ABH - прямоугольный, AB = 13, AH = 5, то по теореме Пифагора находим высоту BH:
7. Находим площадь треугольника ABC:
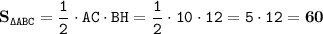
ответ: