1 Действие: (сначала приводим у общему знаменателю 10, умножая числитель и знаменатель второй дроби на 2 и складываем эти дроби)
2 Действие (сначала приводим у общему знаменателю 30, умножая числитель и знаменатель первой дроби на 2 и второй дроби на 3 . Потом расписываем на неправильную дробь т.е 30*2+16=76 в числителе и тоже самое в знаменателе, и вычитаем дроби, но получается дробь которую нужно сократить, т.е разделить и числитель и знаменатель на одно и тоже число, вот мы и делим числитель и знаменатель на 5)
Столов забрали на 26 человек. Сразу можно предложить вариант, что это было 2 стола по 13 человек. Попробуем найти другие варианты.
Предположим, что стол на 13 человек был один. Тогда еще 13 мест нужно получить суммируя по 4 и/или 7 мест. Другими словами, нужно решить уравнение 4x+7y=134x+7y=13 в целых неотрицательных числах.
Задавая yy найдем соответствующие значения xx . Заметим, что 1313 - нечетное число, а 4x4x - четное. Значит, число 7y7y должно быть нечетным, тогда и yy должен быть нечетным. Задавать четные значения yy не имеет смысла.
Если y=1y=1 , то x=\dfrac{13-7}{4}=\dfrac{6}{4}x=413−7=46 - не удовлетворяет условию
При y\geq 3y≥3 левая часть оказывается больше правой.
Уравнение в целых неотрицательных числах решений не имеет. Значит, такой вариант не реализуется.
Предположим, что столов на 13 человек не было. Тогда все 26 мест нужно получить суммируя по 4 и/или 7 мест. То есть, нужно решить уравнение 4x+7y=264x+7y=26 в целых неотрицательных числах.
Задавая yy найдем соответствующие значения xx . Заметим, что 2626 и 4x4x - четные числа. Значит, и число 7y7y должно быть четным. Тогда и yy должен быть четным. Задавать нечетные значения yy не имеет смысла.
Если y=0y=0 , то x=\dfrac{26}{4}x=426 - не удовлетворяет условию
Если y=2y=2 , то x=\dfrac{26-7\cdot2}{4}=\dfrac{12}{4}=3x=426−7⋅2=412=3 - решение соответствует 3 столам на 4 места и 2 столам на 7 мест
При y\geq 4y≥4 левая часть оказывается больше правой.
Таким образом, всего возможно две ситуации:
- это было 2 стола на 13 человек
- это было 3 стола на 4 человека и 2 стола на 7 человек, итого 3+2=5 столов
Пошаговое объяснение:
1 Действие: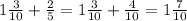
(сначала приводим у общему знаменателю 10, умножая числитель и знаменатель второй дроби на 2 и складываем эти дроби)
2 Действие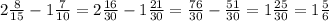
(сначала приводим у общему знаменателю 30, умножая числитель и знаменатель первой дроби на 2 и второй дроби на 3 . Потом расписываем на неправильную дробь т.е 30*2+16=76 в числителе и тоже самое в знаменателе, и вычитаем дроби, но получается дробь которую нужно сократить, т.е разделить и числитель и знаменатель на одно и тоже число, вот мы и делим числитель и знаменатель на 5)
Найдем на сколько человек забрали столов:
59-33=2659−33=26
Столов забрали на 26 человек. Сразу можно предложить вариант, что это было 2 стола по 13 человек. Попробуем найти другие варианты.
Предположим, что стол на 13 человек был один. Тогда еще 13 мест нужно получить суммируя по 4 и/или 7 мест. Другими словами, нужно решить уравнение 4x+7y=134x+7y=13 в целых неотрицательных числах.
Задавая yy найдем соответствующие значения xx . Заметим, что 1313 - нечетное число, а 4x4x - четное. Значит, число 7y7y должно быть нечетным, тогда и yy должен быть нечетным. Задавать четные значения yy не имеет смысла.
Если y=1y=1 , то x=\dfrac{13-7}{4}=\dfrac{6}{4}x=413−7=46 - не удовлетворяет условию
При y\geq 3y≥3 левая часть оказывается больше правой.
Уравнение в целых неотрицательных числах решений не имеет. Значит, такой вариант не реализуется.
Предположим, что столов на 13 человек не было. Тогда все 26 мест нужно получить суммируя по 4 и/или 7 мест. То есть, нужно решить уравнение 4x+7y=264x+7y=26 в целых неотрицательных числах.
Задавая yy найдем соответствующие значения xx . Заметим, что 2626 и 4x4x - четные числа. Значит, и число 7y7y должно быть четным. Тогда и yy должен быть четным. Задавать нечетные значения yy не имеет смысла.
Если y=0y=0 , то x=\dfrac{26}{4}x=426 - не удовлетворяет условию
Если y=2y=2 , то x=\dfrac{26-7\cdot2}{4}=\dfrac{12}{4}=3x=426−7⋅2=412=3 - решение соответствует 3 столам на 4 места и 2 столам на 7 мест
При y\geq 4y≥4 левая часть оказывается больше правой.
Таким образом, всего возможно две ситуации:
- это было 2 стола на 13 человек
- это было 3 стола на 4 человека и 2 стола на 7 человек, итого 3+2=5 столов
ответ: 2 или 5 столов