Практическое занятие № 7 Задание. Даны координаты четырех точек А (х1; у1; z1), В (х2; у2; z2), С (х3; у3; z3), D (х4; у4; z4). Необходимо найти:
1) уравнение плоскости Q, проходящей через точки А, В, С;
2) канонические уравнения прямой АВ;
3) уравнение плоскости G, проходящей через точку D перпендикулярно прямой АВ;
4) расстояние от точки D до плоскости Q.

5. А (–6; –4; 2); В (5; –2; –1); С (5; 6; –4); D (2; 8; 6);

Пошаговое объяснение:

1)уравнение плоскости Q, проходящей через точки

А (–6; –4; 2);

В (5; –2; –1);

С (5; 6; –4);

для составления уравнения плоскости используем формулу

(x -(-6))(2*(-6) - (-3)*10) - (y -(-4))(11*(-6) -(-3)*11 ) + (z -2)(11*10 -2*11) = 0

18(x -(-6)) + 33(y - (-4)) +  88(z - 2) = 0

и вот мы получаем уравнение плоскости Q

Q : 18x + 33y + 88z +64 = 0

2) канонические уравнения прямой АВ.  А(–6; –4; 2); В(5; –2; –1);

формула канонического уравнения прямой

наша формула прямой

3) уравнение плоскости G, проходящей через точку D(2; 8; 6) перпендикулярно прямой АВ

будем искать прямую в виде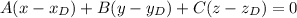

здесь А, В, С - координаты направляющего вектора.

поскольку G ⊥ АВ, то нормаль АВ будет направляющим вектором для G ⇒ s = n = (11, 2, -3)

и вот формула

G : 11y + 2y - 3z -20 =0

4) расстояние от точки D(2; 8; 6) до плоскости Q : 18x + 33y + 88z +64=0

для расчета нам потребуется

А = 18;  В = 33;  С = 88;  D = 64;