Пределы
Х к бесконечности
((х+2)/х)^(3-2х)

Пошаговое объяснение:

Сразу проглядывает тут Второй Замечательный Предел: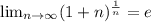

Значит, надо пытаться к нему приводить:

Преобразуем выражение:

Получили ВЗП

Теперь воспользуемся такой штукой: перейдём от предела степени к степени предела, т.е., к этому:

Решаем верхний предел, получаем ответ: