Тогда уравнение касательной в точке а к графику функции - это уравнение
(если надо вывести, напишите в комментариях)
Найдём производную функции:
Запишем уравнение касательной в точке а
Если прямая вида , параллельна оси абсцисс, то коэффициент наклона (k) равен 0
В нашем уравнении коэффициент наклона (множитель перед х) - 4a-6 и он должен быть равен 0 (так как касательная параллельна оси абсцисс. Решим уравнение
При таком значении касательная параллельна оси абсцисс (см. картинку)
при x = 1.5
Пошаговое объяснение:
Пусть это значение - а
Тогда уравнение касательной в точке а к графику функции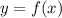 - это уравнение
- это уравнение 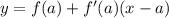
(если надо вывести, напишите в комментариях)
Найдём производную функции:
Запишем уравнение касательной в точке а
Если прямая вида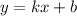 , параллельна оси абсцисс, то коэффициент наклона (k) равен 0
, параллельна оси абсцисс, то коэффициент наклона (k) равен 0
В нашем уравнении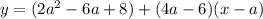 коэффициент наклона (множитель перед х) - 4a-6 и он должен быть равен 0 (так как касательная параллельна оси абсцисс. Решим уравнение
коэффициент наклона (множитель перед х) - 4a-6 и он должен быть равен 0 (так как касательная параллельна оси абсцисс. Решим уравнение
При таком значении касательная параллельна оси абсцисс (см. картинку)