Выразим из первого и второго уравнения y и z через x. Домножим первое на 5, второе на 3 и сложим:
Теперь домножим второе на 2 и сложим:
y и z линейно зависят от x, то есть на каждый найденный x приходится ровно один y и ровно один z. Значит, если подставит в третье уравнение y и z, оно должно иметь несколько решений относительно x. Также раскроем скобки и сгруппируем всё, что с х, в одной стороне, а остальное — в другой:
Если 16 - a² = 0 ⇔ a = ±4:
При a = 4 0·x = 0 — бесконечно много решений, подходит.
4
Пошаговое объяснение:
Выразим из первого и второго уравнения y и z через x. Домножим первое на 5, второе на 3 и сложим:
Теперь домножим второе на 2 и сложим:
y и z линейно зависят от x, то есть на каждый найденный x приходится ровно один y и ровно один z. Значит, если подставит в третье уравнение y и z, оно должно иметь несколько решений относительно x. Также раскроем скобки и сгруппируем всё, что с х, в одной стороне, а остальное — в другой:
Если 16 - a² = 0 ⇔ a = ±4:
При a = 4 0·x = 0 — бесконечно много решений, подходит.
При a = -4 0·x = -8 — решений нет, не подходит.
При всех остальных a: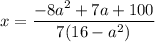
Каждый a задаёт ровно один x, что не подходит.