Вычислим в столбик первый и третий варианты ответа, получим соответственно 12 и 11.
Далее произведем оценку второго и четвертого вариантов:
2: < , то есть данное число чуть больше 11 (т.к. = 11)
4: < , то есть данное число чуть больше 12 (т.к. = 12)
Точка А находится ближе к точке 11, визуально она соответствует числу, меньшему 12, а значит варианты 1 и 4 отпадают. Остается сравнить между собой 2 и 3 варианты:
То есть третий вариант, численно равный 11,8, больше второго, и визуально ближе к середине отрезка.
Эти числа не взамнопросты, так как в их разложении присутствуют одинаковые множители, или, что то же самое, их НОД не равен 1. По предыдушему, если числа взаимно просты, то в их разложении нет общих множителей, а это значит, по определению НОК, что он равен их произведению. Если бы это было не так, то это бы значило, что в разложениях множители повторяются, то есть числа не взаимно просты. ответ на задачу 3 - нет (контрпример: , хотя они не взамнопросты), на задачу 4 - да. Да, так как 3 и 4 взаимно просты.
ответ: ответ №3
Пошаговое объяснение:
Вычислим в столбик первый и третий варианты ответа, получим соответственно 12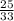 и 11
и 11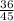 .
.
Далее произведем оценку второго и четвертого вариантов:
2: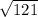 <
< 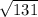 , то есть данное число чуть больше 11 (т.к.
, то есть данное число чуть больше 11 (т.к. 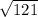 = 11)
= 11)
4: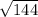 <
< 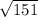 , то есть данное число чуть больше 12 (т.к.
, то есть данное число чуть больше 12 (т.к. 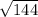 = 12)
= 12)
Точка А находится ближе к точке 11, визуально она соответствует числу, меньшему 12, а значит варианты 1 и 4 отпадают. Остается сравнить между собой 2 и 3 варианты:
То есть третий вариант, численно равный 11,8, больше второго, и визуально ближе к середине отрезка.
Эти числа не взамнопросты, так как в их разложении присутствуют одинаковые множители, или, что то же самое, их НОД не равен 1.