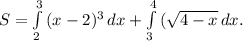Даны 2 функции: и .
первая - кубическая парабола, сдвинутая на 2 единицы в область положительных значений аргумента, функция возрастает,
вторая - ветвь параболы по оси Ох, функция убывает.
Это означает, что графики этих функций пересекаются внутри заданной области, фигура состоит из двух частей.
Находим крайние точки фигуры как точки пересечения с осью Ох при у = 0.
Правая точка. √(4 - x) = 0, возводим в квадрат обе части: х = 4.
Левая точка. (x - 2)^3 = 0, извлекаем кубический корень из обеих частей: х = 2.
Теперь находим точку пересечения: (x - 2)^3 = √(4 - x). Отсюда видно, что корень равен х = 3.
Теперь можно определить искомую площадь как сумму двух интегралов:
Даны 2 функции: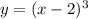 и
и 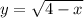 .
.
первая - кубическая парабола, сдвинутая на 2 единицы в область положительных значений аргумента, функция возрастает,
вторая - ветвь параболы по оси Ох, функция убывает.
Это означает, что графики этих функций пересекаются внутри заданной области, фигура состоит из двух частей.
Находим крайние точки фигуры как точки пересечения с осью Ох при у = 0.
Правая точка. √(4 - x) = 0, возводим в квадрат обе части: х = 4.
Левая точка. (x - 2)^3 = 0, извлекаем кубический корень из обеих частей: х = 2.
Теперь находим точку пересечения: (x - 2)^3 = √(4 - x). Отсюда видно, что корень равен х = 3.
Теперь можно определить искомую площадь как сумму двух интегралов: