Гири по 20 кг в сумме дают число, которое кончается на 0. Гири по 5 кг в сумме дают число, которое кончается на 0 или на 5. Только гири по 3 кг дают другие числа. Масса 137 кончается на 7. Возможные варианты: 1) 9 гирь по 3 кг, всего 27. Остальные 11 гирь дают 110 кг. Гирь по 5 кг должно быть чётное количество, а по 20 нечетное. 1*20+10*5=20+50=70 3*20+8*5=60+40=100 5*20+6*5=100+30=130 Не получается. 2) 1 гиря 5 кг и 4 гири по 3 кг. Всего 5+4*3=5+12=17 кг. Остальные 15 гирь дают 120 кг. Число гирь 5 кг опять чётное, а 20 кг опять нечетное. 1*20+14*5=20+70=90 3*20+12*5=60+60=120 - Бинго! ответ: 3 гири по 20 кг, 13 по 5 кг и 4 по 3 кг.
Гири по 5 кг в сумме дают число, которое кончается на 0 или на 5.
Только гири по 3 кг дают другие числа.
Масса 137 кончается на 7. Возможные варианты:
1) 9 гирь по 3 кг, всего 27.
Остальные 11 гирь дают 110 кг.
Гирь по 5 кг должно быть чётное количество, а по 20 нечетное.
1*20+10*5=20+50=70
3*20+8*5=60+40=100
5*20+6*5=100+30=130
Не получается.
2) 1 гиря 5 кг и 4 гири по 3 кг.
Всего 5+4*3=5+12=17 кг.
Остальные 15 гирь дают 120 кг.
Число гирь 5 кг опять чётное, а 20 кг опять нечетное.
1*20+14*5=20+70=90
3*20+12*5=60+60=120 - Бинго!
ответ: 3 гири по 20 кг, 13 по 5 кг и 4 по 3 кг.
Пошаговое объяснение:
1) Преобразовать в многочлен стандартного вида выражение:
А)х2 – 3х + 4 + 6=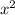
+3x+10
б)(3х - 1) х =3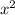
-x
в)-2х (х3 – 3х + 1)=-2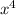
-3
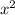+1
г)(х + 3)(х2 - 3х + 9)=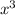
-3
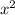+9x+3
2)Упростить выражение:
а)4у2 (уn + 2n2) – 3уn (5y2 +3yn)=4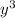
n+8
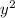
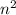-15
б)6t (2t + 4) – (t + 3)(t – 7)=12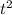
+24t-
3)Найти значение выражения
11ab + 2a - b - 8 при a = 0,21 и b = -3
11ab + 2a - b - 8=11*0.21*(-3)+2*0.21+3-8= -6.93+0.42-5=-11.51.
4)Решить уравнение:
(3x + 4)(4х - 3) – 36 = (2х + 5)(6х - 7)
12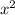
-9x+16x-12-36=12
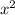-14x+30x-35
-9x+16x-12-36+14x-30x+35=0
-9x-12=0
9x+12=0
9x=-12
x=-12/9
x=-4/3
x=-1 1/3
5. Представить в виде произведения многочлены
А) 4(k-2)+k(k-2) =4k-8+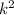
-2k=
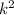+2k-8
Б) 2-5r+2r-5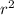
=-5
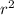-3r+2
.