Прикреплено в файле ))) заранее

Переведем длину ребра куба из дециметров в сантиметры, и сравним ее с длиной ребра выемки:

1 дм = 10 см.

Т.к. длина ребра куба больше длины ребра выемки, то его объем больше чем объем выемки, и выемка будет полностью располагаться внутри него. Куб полностью заполнен мрамором, значит выемка из него, так же будет заполнена мрамором, и не будет полой. Найдем объем выемки:

8 * 8 * 8 = 512 (см3).

Переведем ответ в кубические метры:

512 * 0.000001 = 0,000512 (м3).

ответ: объем выемки составляет 0,000512 кубических метра.

Провести плоскость через прямую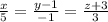  

и точку Mo(4; 3; 1).

Решение. Убедимся, что точка  не лежит на прямой, данной в условии:

 4/5 ≠ (3-1)/-1 ≠ (1+3)/3.

Из уравнения данной прямой следует, что точка M1(0;1; -3)  лежит на этой прямой.

Пусть M(x;y;z)  - произвольная точка искомой плоскости, тогда векторы MoM(x-4; y-3; z-1), M1Mo(4; 2; 4)  и s(5; -1; 3) компланарны. Следовательно,  их смешанное произведение равно нулю:

x-4      y-3      z-1|       x-4         y-3

 4         2          4|        4            2

 5        -1           3|        5           -1   =  

= 6(x-4) + 20(y-3) - 4(z-1) - 12(y-3) + 4(x-4) - 10(z-1) =

= 6x -24 +20y - 60 - 4z + 4 - 12y + 36 + 4x - 16 - 10z + 10 =

= 10x + 8y - 14z - 50 = 0   или, сократив на 2:

5x + 4y - 7z - 25 = 0.

Таким образом, нормальный вектор искомой плоскости равен:

(5; 4; -7).