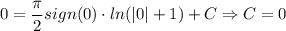На мн-ве подынтегральная функция, очевидно, определена везде, кроме точки x=0.
А тогда, если доопределить подынтегральную функцию в нуле значением , она станет непрерывной по x на промежутке . При этом, очевидно, на значение интеграла такое доопределение не влияет.
По подынтегральная функция, очевидно, непрерывна.
А тогда, согласно теореме о дифференцировании по параметру, получим:
Пошаговое объяснение:
На мн-ве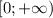 подынтегральная функция, очевидно, определена везде, кроме точки x=0.
подынтегральная функция, очевидно, определена везде, кроме точки x=0.
А тогда, если доопределить подынтегральную функцию в нуле значением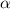 , она станет непрерывной по x на промежутке
, она станет непрерывной по x на промежутке 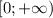 . При этом, очевидно, на значение интеграла такое доопределение не влияет.
. При этом, очевидно, на значение интеграла такое доопределение не влияет.
По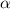 подынтегральная функция, очевидно, непрерывна.
подынтегральная функция, очевидно, непрерывна.
А тогда, согласно теореме о дифференцировании по параметру, получим:
Тогда
Очевидно для начального условия взять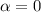 :
:
А тогда