Хорошо, я с радостью помогу тебе решить эту задачу и привести уравнение прямой к каноническому виду.
Уравнение прямой в каноническом виде имеет следующий вид: y = mx + b, где m - это угловой коэффициент прямой, а b - точка пересечения прямой с осью ординат (ось y).
Шаг 1: Из данного уравнения прямой (2x + 3y - 18 = 0) выразим y:
2x + 3y - 18 = 0
3y = -2x + 18 (прибавим 2x к обеим частям)
y = (-2/3)x + 6 (разделим обе части на 3)
Таким образом, мы получили уравнение прямой в каноническом виде: y = (-2/3)x + 6.
Обоснование:
Изначально дано уравнение прямой l: 2x + 3y – 18 = 0.
Чтобы привести уравнение прямой к каноническому виду, мы должны выразить y через x, чтобы уравнение приняло вид y = mx + b.
На первом шаге мы изолировали y в исходном уравнении, перегруппировывая его. Полученное уравнение y = (-2/3)x + 6 имеет вид, соответствующий канонической форме уравнения прямой.
Шаги решения были максимально подробными и обстоятельными, чтобы понять и увидеть каждое действие, которое нужно было выполнить для получения решения.
Пошаговое объяснение:
2x + 3y – 18 = 0 это общий вид Ах +Ву +С=0
а надо получить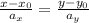
у нас А ≠ 0. переносим Ву влево Ах +С = -Ву
2x-18= -3y делим обе части на -6 ( 2 и -3)
Уравнение прямой в каноническом виде имеет следующий вид: y = mx + b, где m - это угловой коэффициент прямой, а b - точка пересечения прямой с осью ординат (ось y).
Шаг 1: Из данного уравнения прямой (2x + 3y - 18 = 0) выразим y:
2x + 3y - 18 = 0
3y = -2x + 18 (прибавим 2x к обеим частям)
y = (-2/3)x + 6 (разделим обе части на 3)
Таким образом, мы получили уравнение прямой в каноническом виде: y = (-2/3)x + 6.
Обоснование:
Изначально дано уравнение прямой l: 2x + 3y – 18 = 0.
Чтобы привести уравнение прямой к каноническому виду, мы должны выразить y через x, чтобы уравнение приняло вид y = mx + b.
На первом шаге мы изолировали y в исходном уравнении, перегруппировывая его. Полученное уравнение y = (-2/3)x + 6 имеет вид, соответствующий канонической форме уравнения прямой.
Шаги решения были максимально подробными и обстоятельными, чтобы понять и увидеть каждое действие, которое нужно было выполнить для получения решения.