Тут нужно воспользоваться формулой Бернулли, описывающей вероятность того, что в n независимых испытаниях, в каждом из которых вероятность наступления события равна p, событие наступит ровно k раз.
Будем решать задачу от обратного. Найдем вероятность противоположного события, а именно: вероятность того, что неправильный ответ будет зафиксирован 0 или 1 раз.
Для такой задачи
Тогда вероятность того, что ответ будет зафиксирован 0 или 1 раз равна
Тогда вероятность того, что неправильный ответ появится хотя бы 2 раза:
Таким образом, можно сказать, что вероятность того, что детектор зафиксирует хотя бы 2 неправильных ответа, сильно близка к 1
0.99999999998134765625
Пошаговое объяснение:
Тут нужно воспользоваться формулой Бернулли, описывающей вероятность того, что в n независимых испытаниях, в каждом из которых вероятность наступления события равна p, событие наступит ровно k раз.
Будем решать задачу от обратного. Найдем вероятность противоположного события, а именно: вероятность того, что неправильный ответ будет зафиксирован 0 или 1 раз.
Для такой задачи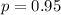
Тогда вероятность того, что ответ будет зафиксирован 0 или 1 раз равна
Тогда вероятность того, что неправильный ответ появится хотя бы 2 раза:
Таким образом, можно сказать, что вероятность того, что детектор зафиксирует хотя бы 2 неправильных ответа, сильно близка к 1
32
Пошаговое объяснение:
1) Пусть х - данное натуральное число.
2) Когда к нему справа приписали 4, то это натуральное число превратилось в 10х (добавился ещё 1 разряд).
3) Составляем уравнение и решаем его:
(10х + 4) : (х + 4) = (х + 4 - 27)
10х + 4 = х^2 - 23х + 4х - 92
х^2 - 29 х - 96 = 0
х = 29/2 ± √ [(841/4) + 96] = 29/2 ± √ (1225/4) = 29/2 ± 35/2.
х = 29/2 + 35/2 = 64/2 = 32.
Отрицательный корень отбрасываем, так как натуральными числами являются только положительные числа.
ПРОВЕРКА:
а) данное число равно 32;
б) к нему справа приписали 4 - стало 324.
в) разделили на (32+4):
324 : 36 = 9;
г) 9 меньше, чем 36 на 27.
Всё сходится.
ответ: 32.